Квантование и дискретизация сигнала

В процессе преобразования сигналов измеряемой информации используется замена переменного сигнала дискретным. При этом выделяется 2 процедуры решения этой задачи:

1. квантование сигнала;

2. дискретизация.

Сущность квантования непрерывного сигнала по уровню заключается в том, что все возможные значения непрерывной величины заменяют на определенные фиксированные значения, которые называют уровнями квантования.

Квант– разница между двумя соседними уровнями, может быть постоянным или изменяться по какому-либо закону (рис. 32).

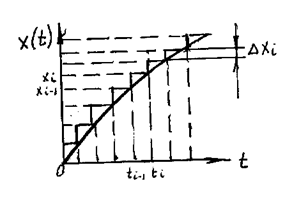
Рис. 32. Пример квантованного сигнала

Вполне естественным является тот факт, что, округляя значение x(t) до ближайшего уровня мы, тем самым, вводим методическую погрешность преобразования (квантования):

,

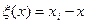где x_i- соответствующий уровень квантования;

х- текущее значение непрерывной величины.

Данная погрешность в основном определяется двумя аспектами:

1. величиной шага квантования. Очевидно, что с уменьшением разницы между уровнями данная погрешность будет уменьшаться;

2. характер квантования (равномерный или неравномерный) и соотношение характера квантования с видом самой функции x(t).

Оценка погрешности равномерного квантования.

Пусть Dх₁=Dх₂=…=Dх, тогда:

Dх=х/N,

где х- диапазон изменения входной величины;

N- общее число интервалов квантования.

При оценке погрешности можно отметить, что в данном случае максимальная погрешность квантования определяется, как половина значения Dх, то есть наибольшая погрешность не превышает половины интервала квантования.

Число ступеней квантования, необходимых для обеспечения требуемой погрешности:

.!!!!!!!!!!

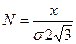Дискретизация- процедура преобразования непрерывного сигнала в дискретный. То есть, это замены непрерывной по аргументу функции x(t) функцией x(t_i) дискретного аргумента t_i, то есть в заданные моменты дискретизации t_i фиксируются значения реальной функции x(t). При этом теряется информация о значении функции в любых других моментах времени. Шагом дискретизации называется промежуток времени между соседними значениями аргумента (рис. 33).

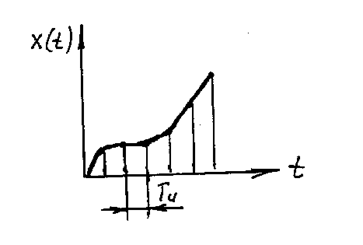
Рис. 33. Пример шага дискретизации

Для записи дискретного сигнала как функции времени используют следующую запись:

.

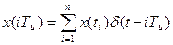Дискретизация может быть равномерной и неравномерной:

— условие равномерности дискретизации – Т_и=const;

— условие неравномерности дискретизации – Т_и=var.

Технически квантование осуществляется с помощью аналого-цифровых преобразователей.

Дискретизация может осуществляться различным путем. Одна из процедур заключается в том, что непрерывный сигнал x(t) пропускают через ключ, который замыкается на очень короткое время в моменты t_i (i=1, 2, …). При этом реализуется совокупность мгновенных значений функции x(iT_и).

Особую важность представляет вопрос восстановления функции по отсчетам x(iT_и). Восстанавливаемая функция строится как временная сумма некоторых функций j_i называемых базисными:

,

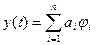где a_i- некоторые коэффициенты полинома.

В качестве базисных выбирают систему таких функция, для которых выполняется условие:

.

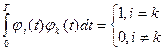Такие функции называются ортогональными, где (0; Т) область существования функции. Коэффициенты a_i выбирают из условия минимизации погрешности:

.

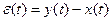При этом в качестве критерия минимума можно взять различные составляющие функции погрешности. К числу критериев можно отнести минимум среднего квадратического отклонения погрешности в пределах диапазона, минимум максимального отклонения, минимум среднего значения математического ожидания и т.п.

Чаще всего выбирают минимум среднеквадратического отклонения погрешности в пределах диапазона. В этом случае при выборе в качестве базисных функций ортогональных функций коэффициенты a_i определяют аналогично коэффициентам Фурье:

.

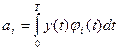В качестве базисных функций могут быть взяты тригонометрические функции, а также различные полиномы: Чебышева, Лежандра и пр. Считается наиболее перспективным применение в качестве аппроксимирующих функций степенных полиномов.

В измерительной технике и в теории связи широко применяется подход Котельникова к построению функции восстановления.

Теорема Котельникова: функция х(t), удовлетворяющая условиям Дирихле и обладающая ограниченным спектром частот w_с в случае ее дискретизации циклически периодом:

; ,

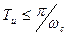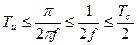может быть восстановлена по этой совокупности без погрешности.

Теорема доказывается с помощью преобразования Фурье.

Так как спектр ограничен частотой w_с, то:

. (*)

Разложив в ряд Фурье S(jw) можно записать:

;

.

Если провести замену переменной в выражении (*) t=-iT_и, то:

. (**)

Из выражения (**) видно, что:

;

. (***)

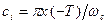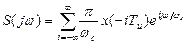Группируя члены в выражении (*), предварительно подставив в него выражение (***) получим:

.

Это выражение часто называют радом Котельникова с коэффициентами равными мгновенным значениям сигнала.

Часто ряд записывают в виде:

.

Согласно этому выражению вводится понятие функции отсчета:

.

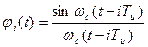Данная функция имеет определенную конфигурацию и является, по сути, реакцией идеального ФНЧ на единичный импульс. В моменты времени t=(i±k)T_и, где к- целое число, функция обращается в нуль.

Для восстановления функции x(t) необходимо подобрать не фильтре низких частот с верхней границей w_с последовательность единичных импульсов с амплитудами, соответствующими мгновенным значениям функции в момент времени iT_и.

При выборе интервала Т_и или при определении необходимого числа мгновенных значений и в случае замены непрерывных функций дискретными, необходимо помнить, что для получения достоверной однозначной оценки функции при ее дальнейших разложениях в ряд Фурье и восстановлении следует обеспечивать условие теоремы Котельникова, что в пересчете на номера гармоник выглядит следующим образом:

,

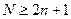где N- число интервалов дискретизации (число дискретных значений в пределах диапазона);

n- номер гармоники, которой соответствует предельная частота спектра реального сигнала (w_с).

Если это условие не выполняется, то однозначно характеризовать требуемое число гармоник не представляется возможным. В этом случае при наличии априорной информации о реальных источниках гармонических составляющих сигнала можно решить данную задачу с определенными допущениями. Но это не всегда возможно. В этом случае во внимание принимается то, что каждая гармоника включает в себя группу гармоник. В зависимости от реальных N и n составляются соответствующие таблицы, в которых указываются данные группы гармоник.

Дата добавления: 2014-01-06