Корреляционный анализ. Корреляционные характеристики относятся к наиболее широко применяемым при проведении вероятностного анализа случайных величин и процессов

Корреляционные характеристики относятся к наиболее широко применяемым при проведении вероятностного анализа случайных величин и процессов. С помощью корреляционного анализа решаются следующие задачи:

— выделение полезных сигналов на фоне помех;

— статистическая идентификация объектов;

— оптимальная фильтрация;

— прогнозирование течения процессов;

— спектральный анализ;

— техническая диагностика;

— научные исследования многофакторных процессов и т.д.

При исследовании стохастической связи между случайными величинами оцениваются коэффициенты корреляции или корреляционные моменты. Для описания случайных процессов применяются корреляционные и взаимные корреляционные функции. Применимость этих характеристик ограничена случаем линейной стохастической связи (при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону).

Определение. В общем случае корреляционная функция является функцией двух аргументов t₁ и t₂ и представляет собой математическое ожидание произведений центрированных значений случайной функции для этих двух аргументов:

.

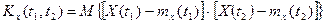Индекс Х в левой части выражения показывает, к какой случайной функции относится корреляционная функция.

Значение корреляционной функции при равных значениях аргументов t=t₁=t₂ дает дисперсию случайного процесса:

.

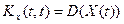Если случайный процесс стационарен, то корреляционная функция является функцией лишь разности аргументов:

,

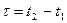а не их абсолютных значений.

.

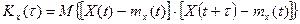Кроме рассмотренных корреляционных функций применяется временная корреляционная функция, предполагающая усреднение по времени одной реализации случайного процесса:

.

Нормированная корреляционная функция определяется как:

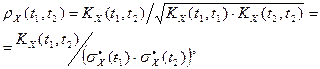
где 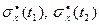- среднее квадратическое значение сигнала.

Для стационарного случайного процесса:

,

где 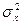- дисперсия процесса (сигнала).

Для характеристики взаимосвязи между значениями двух случайных процессов X(t) и Y(t) служит взаимная корреляционная функция:

.

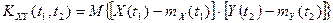Нормированная взаимная корреляционная функция:

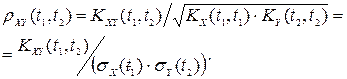
Для стационарных случайных процессов:

;

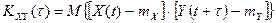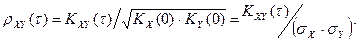
Нормированная корреляционная функция и нормированная взаимная корреляционная функция по смыслу аналогичны коэффициенту корреляции между случайными величинами, но в отличии от него они зависят от двух аргументов t₁ и t₂ и не являются постоянной величиной.

Если стационарные случайные процессы являются совместно эргодическими по отношению к взаимной корреляционной функции, то она определяется так:

.

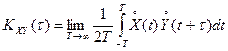Для реальных сигналов оцениваются оценки корреляционной и взаимной корреляционной функций. При измерении оценки функции корреляции 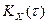или взаимной корреляции 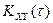необходимо осуществить взаимный сдвиг (задержку) сигнала реализации на время t, перемножить два сигнала x(t) и x(t+t) или x(t) и y(t+t), а затем усреднить произведение в течении достаточно продолжительного времени.

На практике часто используются следующие оценки:

1.

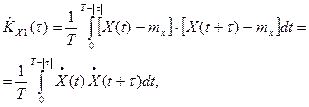
где .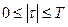

Для интервалов сдвига 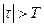функция .

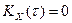2.

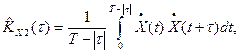
где .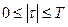

При экспериментальном определении статистической корреляционной функции 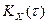ее значения вычисляются для ограниченного диапазона значений аргумента t – от 0 до t_max.

,

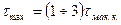где 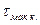- максимальный интервал корреляции исследуемого случайного процесса.

Вторая оценка 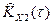- характеризуется большей среднеквадратической погрешностью, чем .

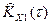Аналогично определяются оценки для взаимной корреляционной функции.

Дата добавления: 2014-01-06