Вероятность и информация. Статистические меры информации

Информация. Термины и определения. Меры информации.

I. 2. Теория информации

В этой части мы рассматриваем область, именуемую связью (информатикой), точнее рассмотрим шире – вопросы выработки, передачи, приема и обработки информации. Для чего прежде выясним, что такое информация.

Понятие «информация» наряду с материей и энергией является первичным понятием нашего мира и поэтому в строгом смысле не может быть определено.

Информация – это совокупность содержательных сведений (данных) заключенных в том или ином сообщении и имеющих вид знаков или сигналов, заранее не известных человеку (или машине) принимающему это сообщение. Таким образом, информация - это сообщение представленное последовательностью знаков или символов (сигналов). Знаки, символы, сигналы – материальные объекты, а сигналы, кроме того, еще и динамические процессы. Сообщением может быть телеграмма, текст, речь и т.д., т.е. сообщение может иметь различную форму: иметь вид сигнала, графики или текста, но отличительной особенностью его является то, что оно имеет информационную часть выраженной энергетической составляющей (следует отметить малые величины этой энергии).

Каждый вид сообщения, переданный знаками или сигналами, может иметь только определенную часть всех сведений, всей информации. Т.о. сообщение (его информационная часть) имеет меру, а вид сообщения может иметь ограничение по передаче информации, т.е. ограничение по количеству передаваемой информации.

В связи с этим применяются различные способы преобразования сообщений, такие, как дискретизация, кодирование, модуляция с целью получения оптимального сигнала с наибольшей информационной нагрузкой. Т.о. информация имеет объем – количественную меру, целесообразность – структурную меру, ценность, полезность – семантическую меру, меру неопределенности или вероятность получения фрагментов информации - статистическую меру.

При вероятностном подходе информация рассматривается как сообщение об исходе случайных событий, реализации случайных величин и функций, а количество ин-
формации ставится в зависимость от априорных вероятностей этих событий, величин, функций.

Когда получается сообщение о часто встречающихся
событиях, вероятность появления которых стремится к единице, т. е. к показателю полной достоверности, то такое
сообщение мало информативно. Столь же мало информативны сообщения о противоположных событиях (антисо-
бытиях), вероятности которых стремятся к нулю и которые,
следовательно, почти невозможны. Например, событие
«часы идут» имеет вероятность р = 1, тогда как антисобы-
тие «часы не идут» имеет вероятность q = 1 — р = 0.

Событие и антисобытие составляют одно двоичное - однопредметное событие. Может быть, также двоичное двухпредметное событие, заключающееся в выборе одного из двух возможных предметов, например, черного или белого шара из урны, «герба» или «решки» на монете.

Большинство видов информации можно свести к двоичным явлениям «да — нет» и к паре: «событие — антисобытие». Именно эта пара явлений является простейшим и неделимым элементом («квантом») информации (см. табл. 1-1).

Другой вид сообщений составляют двухпредметные двоичные явления, которые распадаются на четыре элементарных акта. Например: 1) вынут белый шар; 2) не вынут белый шар; 3) не вынут черный шар; 4) вынут черный шар.

Могут быть также исключающие друг друга события. Например, если выпал герб, то не может одновременно выпасть решка. Если в цепи установилось напряжение 100в, то не может в той же цепи одновременно существовать
напряжение 12 в.

Будем под событием далее понимать элементарное однопредметное явление, которое может быть с вероятностью от р = 0 до р = 1 или не быть с вероятностью от
q = 1 — р = 1 до q = 1 — р = 0.

Когда р = 0,5 и q = 0,5, то будет иметь место наибольшаянеопределенность в ситуации.

Таблица 1-1

А. Двоичные однопредметные события
Событие	Антисобытие
Дождь идет Снег идет Машина работает Лампа горит Уровень достигнут	Дождь не идет Снег не идет Машина стоит Лампа погашена Уровень не достигнут
Б. Двоичные двухпредметные события
Явление 1	Явление 2
Дождь (толи дождик) идетне идет (толи будет) (то ли нет) Белый шар вынут не вынут	Снег (то ли снег) не идет идет (то ли нет) (то ли будет) Черный шар не вынут вынут

Таблица 1-2

	Исходы опыта	А1	А2	…	Аi	…	Аk
	Значения величины	х1	х2	…	хi	…	хk
	Соответствующие вероятности	р1	р2	…	рi	…	рk

События можно рассматривать как возможные исходы некоторого опыта, причем все исходы составляют ансамбль, или полную группу событий. Последняя характеризуется тем, что сумма вероятности событий в ней равна единице.

р₁ + р₂ + … + р_i + … + р_k = 1

Опытом может быть и изменение случайной величины Х, принимающей различные значения. Тогда каждое определяемое значение имеет смысл исхода, или элементарного события. Вообще событиями х₁, х₂, х₃, …, х_k могут быть k дискретных состояний какой-либо физической системы, например k значений измеряемой величины, k положений регулирующего органа, состояние k элементов производственного оборудования, k потоков денежных средств и т.д. Этому соответствует приведенная таблица (1-2), называемая схемой ансамбля.

В простейшем случае эти события несовместимы. Они
составляют полную группу, в которой обязательно реализуется одно из событий и имеет место условие

В общем случае вероятности не остаются постоянными.
Они могут изменяться во времени, в зависимости от условий
и обстоятельств. Тогда и статистические характеристики
(среднее значение и дисперсия) становятся переменными
величинами. Процессы, описываемые этими величинами,
называются нестационарными в статистическом смысле.

Пример 1-1. Прогнозируется температура на отдаленный день
(для определенности в середине дня). Если на основании каких-либо
данных известно только то, что в заданный день температура не может быть ниже 12˚ и выше 21˚, то приходится пользоваться априорной (до
опытной) равномерной плотностью распределения (рис. 1-1, график а):

х_i......12 13 14 15 16 17 18 19 20 21

р(х_i)...0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1 0,1

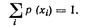
С приближением заданного дня появляется дополнительная ин-
формация, уточняющая распределение вероятностей (рис. 1-1, гра-
фик б). Тогда плотность распределения можно описать
следующим образом:

Х_i.......12˚ 13˚ 14˚ 15˚ 16˚ 17˚ 18˚ 19˚ 20˚ 21˚

p(x_i)... 0 0,05 0,1 0,15 0,2 0,2 0,15 0,1 0,05 0

Естественно, что с наступлением заданного дня и
часа прогнозируемое явление
становится реализованным,
устанавливается определенная температура, например
х = 17˚ (рис. 1-1, график в).
Таким образом, неопределенность снимается полностью и
апостериорное (послеопытное), конечное распределение приобретает следующий вид:

х_i ... 12 13 14 15 16 17 18 19 20 21

р {х_i)... 0 0 0 0 0 1 0 0 0 0

Пример 1-2. Последовательное снятие неопределенности (пере-
дается число (слово) х = 3, выражаемое в двоичном коде как 011),.

Шаг 1. Передается 0; может быть 000, 001; 010, 011.

Шаг 2. Передается 1; может быть 010, 011.

Шаг 3. Передается 1; может быть 011.

Примем теперь неравные начальные вероятности сообщений, как
показано в четвертом столбце табл. 1-3.

Оставшиеся вероятности умножаются на 4/3— величину, обратную
сумме априорных вероятностей подмножества.

Тогда имеем

в пятом столбце 1/
4*4/ 3=1/3; 1/ 4*4/3=1/3; 1/8*4/3=1/6; 1/8*4/3=1/6

В шестом столбце 1/6*3=1/2; 1/6*3=1/2.

В седьмом столбце
I/2*2=1.

Таблица 1-3

Номер п.п.	Кодо- вое слово	Вероятности сообщений
Равные вероят- ности	Априорные вероятно сти	После по - лучения 0 в первом разряде	После по лучения 1 во втором разряде	После по лучения 1 в третьем разряде
		1/8	1/4	1/3
		1/8	1/4	1/3
		1/8	1/8	1/6	1/2
		1/8	1/8	1/6	1/2
		1/8	1/16
		1/8	1/16
		1/8	1/16
7		1/8	1/16

Исходная, полезная информация о процессе, предмете или ином объекте, как правило, содержится в первичных сигналах датчиков (для технических систем). Т.о. физический процесс, однозначно отображающий передаваемое сообщение с заданной точностью и пригодный для его обработки и передачи на расстояние, называется сигналом.

Сигналы могут быть электрическими, акустическими, изменение давления среды и др. процессы (Самостоятельно Темников глава 1-2).

1.2.2. При преобразованиях информация не теряется, хотя некоторые потери в виде ухудшения ее возможны. И можно говорить о законе сохранения информации по аналогии с сохранением энергии.

Отсюда состояние источника информации – сообщение. Передача сообщений в основном производится посредством сигналов – динамических процессов, изменения состояния источника, т.е. сообщение, соответствует изменению какого-либо параметра сигнала. Без такого изменения нет передачи информации. Сигналы принято различать как детерминированные и случайные. Так детерминированный сигнал может быть задан его математической моделью, например:

U(t) = U₀ Cos(ω₀t + φ₀) 1.1.

Случайные же сигналы нельзя предсказать с достаточно малой погрешностью, так как состояние источника информации описывается большим числом факторов (иные из которых могут быть даже неизвестны).

Т.о. любой сигнал, точный закон изменения которого неизвестен, рассматривается как случайный. Случайные сигналы описываются вероятностными (стохастическими) законами, характеризующими распределение вероятностей отдельных значений сигналов для каждого момента времени. Здесь необходимо указать, что источники информации и создаваемые ими сообщения (с следовательно и сигналы)разделяются на дискретные и непрерывные.

При этом дискретные сообщения складываются из конечного множества элементов, создаваемых источником последовательно во времени. Набор элементов (множество всех знаков или символов, сигналов) называется алфавитом источника, а сами элементы (элементарные сообщения) – буквами этого алфавита. Число букв в алфавите называют объемом алфавита. Знаки алфавита можно однозначно сопоставить сигналам другого алфавита. Правила сопоставления – называют кодированием.

1.2.3. В структурной мере информации в свою очередь различают:

- геометрическую меру;

- комбинаторную меру;

- аддитивную меру или меру Хартли, двоичную меру, измеряемую в двоичных единицах – битах. Количество возможной информации определится из выражения:

Q = h^l 1.2.

Т.е. емкость алфавита экспоненциально зависит от длины сообщения (слова, числа). Показательная форма не совсем удобна, поэтому Хартли ввел двоичную меру – бит:

I = log₂Q = log₂h ^l = l log₂h 1.3.

Здесь I – количество информации; h – алфавит (количество букв алфавита); l – длина слова (количество букв в слове). Тогда при l = 1 и h = 2 имеем:

I = log₂2 = 1 (один бит) 1.4.

Существуют также единицы измерения информации дит (основание 10) и нит (основание натуральный логарифм - е).

Статистическая мера информации отражает, таким образом, вероятностный подход к информации. Т.е. количество достоверной информации ставится в зависимость от априорных вероятностей, каких либо событий, величин, функций. События могут быть двоичными одно предметными (дождь идет или не идет), либо двоичными двух предметными (либо дождь идет, либо снег). Двух предметные события образуют полную группу событий (ансамбль), для которой характерно:

Р₁+ Р₂ + Р₃ + … + Р_i + … + Р_k = 1 1.5

или

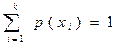1.6.

(назад в оглавление)

Дата добавления: 2014-01-06