Понятие энтропии

Лекция 2.

(самостоятельно)

Как уже было отмечено, информация и энергия имеют весьма близкую аналогию, что заметил еще основоположник теории информации Клод Шеннон. И рассмотрим еще одну аналогию между информацией и энергией. Согласно второму закону термодинамики (закон Больцмана) для замкнутого пространства имеем

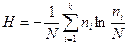2.1.

где N – общее количество молекул в данном объеме пространства; n_i - количество молекул имеющих скорости (а следовательно энергию)

v_i + Dv; n_i/N - частоты или вероятности того, что молекулы имеют скорость v_i + Dv с вероятностью 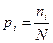и тогда:

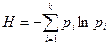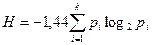или 2.2.

Что и сделал К. Шенон еще в 1948г. выведя формулу для энтропии информации.

Энтропия ансамбля. Ансамблем называется полная группа событий,
или, иначе, поле несовместных событий с известным распре-
делением вероятностей, составляющих в сумме единицу.
Здесь имеется ввиду конечное множество событий и, следовательно, дискретная система состояний, значений, положений и т. д.

Энтропия ансамбля есть количественная мера его не-
определенности, а, следовательно, и информативности.

В статистической теории информации (теория связи),
предложенной Шенноном в 1948г., энтропия количественно
выражается как средняя функция множества вероятностей
каждого из возможных исходов опыта.

Действительно, пусть для какого-то опыта имеется N возможных исходов, из них имеется k – разных и i–ый исход повторяется n_i раз и вносит информацию I_i, Тогда средняя информация, доставляемая одним опытом, определится:

I_ср = 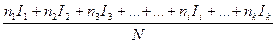2.3.

Или перейдя к логарифмам (выразив в битах), т.к. I_i = - log₂p_i имеем:

I_ср = 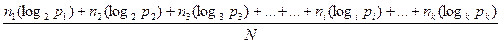2.4.

Или заменив n_i/N = p_i, получим

H = I_ср = -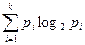 2.5.

Энтропия может быть определена также как среднее количество информации, приходящееся на одно сообщение или математическое ожидание количества информации I для измеряемой величины.

H(x) = M[I(x)] = -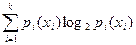 2.12.

Энтропия в функции вероятности исходов H(p), где p = {p₁, р₂, …, р_k} – вектор вероятности исходов, должна удовлетворять следующим требованиям:

1) Функция H(p) должна быть непрерывна на интервале 0 £ p_i ³ 1; т.е. при малых изменениях p величина H меняется мало;

2) Функция H(p) должна быть симметричной относительно аргумента p, т.е. не изменяется при любой перемене мест аргументов р_i;

3) H(p₁, p₂, …, p_k-1, q₁, q₂) = H(p₁, p₂, …, p_k) + p_kH(q₁/p_k, q₂/p_k);

Т.е. если событие x_i состоит из двух событий x_i^’ и x_i^’’ с вероятностями q₁ и q₂, q₁ + q₂ = p_i, то общая энтропия будет равна сумме энтропий – неразветвленной и разветвленной части с весом p при условных вероятностях q₁/p_k и q₂/p_k.

Кроме того, энтропия H характеризуется следующими свойствами:

1. Энтропия всегда неотрицательна, т.к. значения вероятностей выражаются дробными величинами, а их логарифмы – отрицательными величинами, так что энтропия в итоге неотрицательна. (log₂p_i = -(-a) – неотрицательная величина);

2. Энтропия равна нулю в том и только в том крайнем случае, когда одно событие равно единице, а все остальные – нулю. Это тот случай, когда об опыте, событии все заранее известно и результат не приносит никакой новой информации.

3. Энтропия имеет наибольшее значение в том случае, когда все вероятности равны между собой, в этом случае:

p₁ = p₂ = p₃ = … = p_k = 1/k 2.13.

и энтропия в этом случае

H = - log₂ 1/k = log₂k 2.14.

Логарифмическая и статическая мера информации совпадает с аддитивной логарифмической мерой Хартли.

I^` = log₂h 2.15.

Действительно рассмотрим одно предметное событие, которое имеет 2 исхода. Энтропия такого события (для двух неравновероятных событий одного элемента h = 2) равна

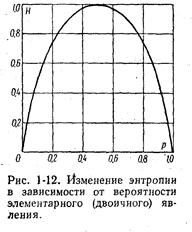
H = - (p₁log₂p₁ + p₂log₂p₂) 2.16.

Она меньше информационной ёмкости одной двоичной единицы, действительно:

А. Пусть имеем равновероятные состояния, тогда -

p₁ = p₂ = 0,5 или p₁ + p₂ = 1;

H=-(0.5log₂0.5+0.5log₂0.5)= - [0.5(-1) + 0.5(-1)] = 1 бит.

Б. Неравновероятные состояния –

p₁ = 0,9 p₂ = 0,1 p₁ + p₂ = 1;

H = -(0.9log₂0.9+0.1log₂0.1)= - [0.9(-0,1520)+0.1(-3,3219)]= =0,46 бит

В. Детерминированное состояние –

p₁ = 1 p₂ = 0 p₁ + p₂ = 1;

H = - (1log₂1+ 0log₂0) = 0 бит

Изменение энтропии H в зависимости от вероятности p однопредметного события представлена на рис. 1-12. Максимум H = 1 достигается при p = 0.5, когда два состояния равновероятны. При вероятностях p = 0 или p = 1, что соответствует полной невозможности или полной достоверности события, энтропия равна нулю.

2.2. Энтропия объединения ( самостоятельно Темников Ф.Е., В.А. Афонин, В.И. Дмитриев. Технические основы информационной техники ).

Объединением называется совокупность двух и более взаимозависимых ансамблей дискретных случайных переменных.

Рассмотрим объединение, состоящее из двух ансамблей Х
и У, например из двух дискретных измеряемых величин,
связанных между собой вероятностными зависимостями.

Схема ансамбля Х

x₁ x_{2 ...} x_{i ...} x _n;

р(x₁,) р(х₂)... р(х_i)... p(х_n).

Схема ансамбля Y:

y₁ y_{2 ….} y_{i ....} y_т,

p (y₁) p (y₂)... p (y_i)... p (y_m)

Схема объединения Х и Y;

	x1	x2	xn
y1 y2 ..... yт	p(x1,y1) p(x1,y2) ................ p (x1, yт)	p(x2 y1) p (x2, y2) ................ p (x2, ym)	p (xn, y1); p (xn, y2); ........... p (xn, ym)

Вероятность совпадения (произведения) совместных зависимых событий Х и Y равна произведению безусловной вероятности р(х) или р(у) на условные вероятности р(у | х) или р(х|у).

Таким образом, имеем:

р(х, у) = р(х) р(у|х) = р(у) р(х|у).

Отсюда находятся условные вероятности

р(у|х) = p(x,y)/р (х) (2-17)

р(х|у) = p(у,x)/р(у) (2-18)

в зависимости от того, какое событие является причиной, а какое — следствием. В нашем случае дискретных переменных Х и Y, частные
условные вероятности могут быть записаны для х = x_k как:

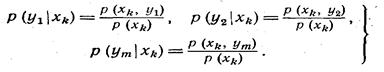
2-19

С объединением связаны понятия безусловной, условной, совместной и взаимной энтропии (табл. 1-4). Их иногда
называют также зависимой, коррелированной и взаимной
энтропией, или т р а н с ф о р м а ц и е й. Введенные понятия можно проиллюстрировать примером
передачи информации по каналу связи по схеме рис. 1-3. Последовательность символов х₁, х₂,..., х_i,..., х_n соз-
даваемая источником, может претерпевать искажения по
пути к приемнику.

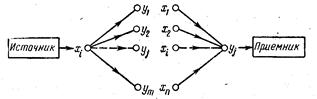Энтропия объединения. Символ х_i может быть принят не только как однозначно
ему соответствующий символ у_j но и как любой из возмож-
ных символов у₁, у₂,..., у_j,..., у_m с соответствующими веро-
ятностями. Рис.1-3. Предача информации по

каналу связи.

Различные виды энтропии в данной схеме имеют, следующий смысл:

Н(Х) — безусловная энтропия источника, или среднее количество информации на символ,
выдаваемое источником;

Таблица 1-4

Н(У) — безусловная энтропия прием-
ника, или среднее количество информации на символ,
получаемое приемником;

Н (Х, Y) — взаимная энтропия системы пере-
дачи-приема в целом, или средняя информация на пару
(переданного и принятого) символов;

Н(У|Х) — условная энтропия У относи-
тельно Х, или мера количества информации в приемнике,
когда известно, что передается Х;

Н(Х|Y) — условная энтропия Х относитель-
но У, или мера количества информации об источнике, когда
известно, что принимается Y.

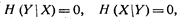Если в системе нет потерь и искажений, то условные
энтропии равны нулю

а количество взаимной информации равно энтропии либо
источника, либо приемника

I(X,Y) = H(X,Y) = H(X) = H(Y)

На основании статистических данных могут быть установлены вероятности событий у₁, у₂,..., у_m при условии,
что имели место события х_i, а именно p(у₁|х_i), р (у₂|х_i),
..., р (у_m|х_i). Тогда частная энтропия будет равна:

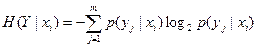(2-20)

Далее нужно подсчитать среднее значение H(Y|Х_i)
для всех переданных символов х_i. Это будет условная энтропия канала

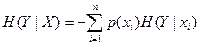
(1-19)

или в развернутом виде

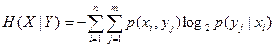(1-20).

Аналогично получается условная энтропия H(Х|Y),
учитывающая условные вероятности

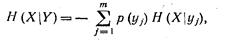(1-21)

или

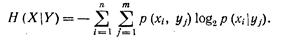(1-22)

Безусловная энтропия ансамбля Х

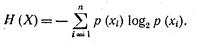(1-23)

Безусловная энтропия ансамбля У

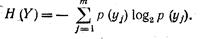(1-24)

Дата добавления: 2014-01-06