Информационная модель канала

Для анализа информационных возможностей удобно
пользоваться обобщенной информационной моделью канала
связи, представленной на рис. 1.6.0. Источник информации
ИИ создает сигналы z, которые после кодирования и моду-
ляции в преобразователе П, превращаются в сигнал х и
поступают в линию связи ЛС. Для удобства сигналы источника будем называть сообщениями, а сигналы х в линии
связи — просто сигналами. В результате действия помех
сигнал у на приемной стороне отличается от х. Помехи имеют
случайный характер и подчиняются статистическим законам. Удобно условно считать, что помехи создаются некоторым воображаемым источником помех ИП с определенными статистическими свойствами и поступают в линию связи
в виде мешающего сигнала "ипсилон". Приемная часть содержит
преобразователь П₂ демодулирующий и декодирующий
принятые сигналы у, и приемник информации ПИ, перера-
батывающий принятые сообщения и. Если канал использу-
ется для передачи кодоимпульсных сигналов, он называ-
ется дискретным. Если же передаваемые сигналы имеют
непрерывный характер, канал называется непрерывным.

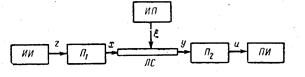
Рис. 1.5 Информационная модель канала связи.

ИИ — источник информации; П ₁, П ₂ — преобразователи
информации; ИП — источник помех; ЛС — линия связи;
ПИ — приемник информации.

Для организации эффективной передачи информации
по каналу требуется решение следующих проблем: определение максимально возможной скорости передачи информации по каналу; разработка кодов, позволяющих увеличить
скорость передачи информации; согласование канала с источником с целью передачи информации с минимальными
потерями. Решение этих задач зависит от свойств источников, уровня и характера помех.

Если уровень помех мал, и искажениями сигнала можно
пренебречь, канал называется каналом без помех.

Отметим, что если источник информации вырабатывает
непрерывную функцию z(t), то путем ее дискретизации по оси
времени t и квантования по уровню методами, описанными
в гл. 2, всегда можно перейти от непрерывного канала к дискретному.

Дискретный источник информации характеризуется алфавитом символов Z = (z₁ z₂,..., z_n}, из которых строятся
сообщения, и вероятностями создания отдельных символов
(которые могут зависеть от того, какие символы были пере-
даны ранее).

Преобразователь П ₁, содержит кодирующее устройство,
преобразующее сообщения z в сигналы х, состоящие из
символов другого алфавита Х = (х_1,х₂,..., х_m) (в частном
случае алфавит Х может совпадать с алфавитом Z, т. е.
т = n) Статистические свойства источника сигнала, которым является вся схема на входе линии связи (источник
информации плюс преобразователь), в общем случае отли-
чаются от статистических свойств источника сообщения.

Далее будет показано, что выбором подходящего кода
можно повысить скорость передачи информации по каналу.

В случае непрерывного сигнала преобразователь П ₁
может содержать модулирующее и преобразующее устрой-
ства, изменяющие статистические характеристики непрерыв-
ного сигнала.

Важнейшей характеристикой канала является пропуск-
ная способность С (её ещё называют ёмкостью канала), которая определяется как наибольшая
возможная скорость передачи информации по данному
каналу:

C = v _x max{ I (Y, Х)} (6-1)

Здесь через v обозначена средняя скорость передачи
по каналу элементарных сигналов (символов). Эту скорость
можно выразить через среднюю продолжительность символов 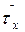передаваемого сигнала:

v_x = 1/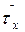

здесь 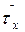- τ_x с чертой сверху, средняя продолжительность символов.

При одинаковой продолжительности τ_x всех передаваемых символов 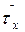= τ_x. Но в ряде случаев символы могут
иметь различную длительность, например при телеграфной
передаче. Тогда вычисляется (не τ_x).

Через max{ I(Y, Х)} обозначено максимально возможное
значение среднего количества информации, содержащееся
в одном символе принятого сигнала. Максимум функционала
I (Y, Х)ищется на множестве функций распределения вероятностей {р(х)} между символами алфавита Х (или других
возможных алфавитов) источника сигналов. Количество
информации I (Y, X), переносимое одним символом, равно
уменьшению степени неопределенности нашего знания о
передаваемом сигнале в результате приема. Неопределенность не устраняется полностью, так как принятый сигнал
может оказаться искаженным помехой. Это количество
информации равно (см. табл. 1-4)

I(Y, Х) = Н (Х) — H (X |Y),

где Н(Х) — энтропия источника сигналов, характеризую-
щая среднюю неопределенность передаваемого сигнала до
приема; H(X|Y) — средняя условная энтропия ансамбля сиг-
налов х при известных принятых сигналах y, характеризующая остаточную среднюю неопределенность передаваемых
сигналов, если известны принимаемые.

Отсюда видно, что среднее количество информации,
содержащееся в символе, зависит от распределения вероят-
ностей между возможными символами, вырабатываемыми
источником сигналов, и от характера и уровня шумов, кото-
рые определяют условную энтропию Н(Х|Y).

Скорость v_x определяется только свойствами канала и не
зависит от источника сигналов. То же самое можно сказать
и о значении max { I (Y, X)}, которое также не зависит от
применяемого источника, так как эта величина есть максимум средней информации, которая может быть передана
по каналу одним символом при оптимальном источнике.

Таким образом, пропускная способность зависит исключительно от канала.

Рассмотрим вопросы передачи сообщений для трех видов
каналов: дискретного канала без помех, дискретного канала
с помехами и непрерывного канала с помехами. Определим
для этих каналов зависимость скорости передачи информации от вида и уровня помех и от вида источника сообщения
(от распределения вероятностей на множестве символов
сообщений источника). Эти вопросы, являющиеся основными
в теории передачи информации, были впервые глубоко
исследованы Шенноном [Л. 6-9].

Если источник сообщений, подключенный к каналу связи, имеет энтропию на символ, равную емкости канала связи, то говорят об информационном согласовании источника с каналом, т.е. Н = с

Если энтропия меньше емкости канала, то источник не согласован (информационно) с каналом, т.е. канал используется не полностью.

Шеннон провел и здесь аналогию между энергетическим согласованием (согласование источника энергии с нагрузкой).

В статистическом смысле, согласование осуществляется с помощью так называемого статистического кодирования. Имеется в виду согласование с помощью кодирующего устройства.

При этом последовательность одних элементарных сигналов (им соответствует 0 или 1) с одной энтропией по определенному закону преобразуется в новую последовательность с энтропией близкой к 1 бит/символ. Новая последовательность может быть также однозначно декодирована на приемной стороне.

В теории информации существуют методы статистического кодирования, позволяющие увеличить энтропию передаваемого сообщения и сократить в нем избыточность (см. формула 1.4.6 (2.18) стр. 13)

Н=1-Н/log m₀ (3.7)

т.к. H_max = log m₀

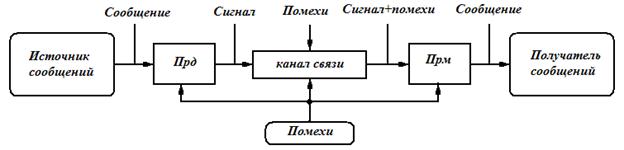
Рис. 1.6.1

Необходимо отметить, что статистическое кодирование вызывает задержку в передаче сообщения (т.к. происходит преобразование кода по определенному закону), что подчас недопустимо для систем работающих в реальном масштабе времени, кроме того, хотя при этом и добиваются оптимального согласования, такое кодирование может ухудшать помехоустойчивость передачи, на фоне устранения избыточности сообщения.

Дата добавления: 2014-01-06