Передача информации при помехах

На рис.1.6.1 приведена схема (структурная) передачи сообщений по каналу с помехами. Шумы (помехи) существенно снижают уверенность в том, что передано то или иное сообщение и тот или иной элемент сообщения.

Возникают две проблемы: повышение эффективности передачи и повышение достоверности (помехоустойчивости) передачи.

Действительно если из-за влияния помех при передаче i –го элемента принят j –ый элемент, то имеем прирост информации

DI_i,j=log₂ (1/P_i) - log₂ (1/P_j(i))= log₂ (P_j(i)/P_i) (3.8)

здесь P_i – безусловная (априорная) вероятность передачи i – го элемента;

P_j(i) – условная вероятность того, что при передаче i-го элемента принят j-ый элемент.

Здесь можно рассматривать два крайних случая:

1) при очень больших шумах [P_j(i)=P_i], тогда из формулы (3.8) имеем

DI_i,j=log₂1=0 (3.9)

т.е., информации нет, принимаются только искаженные сигналы.

2) при отсутствии шумов [P_j(i)=1, если i=j и P_j(i)=0, если j≠i ], тогда из формулы (3.8) имеем:

DI_i,j=log₂ (1/P_i) = - log₂ -P_i= log₂ (P_i) (3.10)

т.е. получаем канал близкий к идеальному (без помех и искажений), где прием сообщений становится достоверным событием, что соответствует формуле 1.2.5 на странице 9.

Скорость передачи информации (в двоичных единицах на символ) в канале с шумами равна (для идеального канала, как уже отмечалось)

Z_c=SP_iP_j(i) DI_i,j=H_i-H_j(I)=H_j-H_i(j) (3.11)

Смотри также формулу 1.5.6 при m₀=1, где

H_i=-SP_i logP_i – энтропия источника;

H_j=-SP_j logP_j – энтропия приемника.

- условные энтропии (3.12)

Для канала без шумов мы имеем

H_i(j)=H_j(i)=0 (3.13)

и тогда после подстановки в 3.11 имеем:

Z_c=H_i=H_j

В канале же с шумами скорость передачи информации

(3.14)

здесь S=1/τ - число передаваемых символов в секунду.

Z_c=H_i-H_j(i) (3.15)

и после подстановки 3.15 в (3.14) имеем

R =S [H_i-H_j(i)] (3.16)

Т.е. скорость в канале с шумами есть разница между переданной и потерянной информацией вследствие действия помех. (см. рис. 1.7.1)

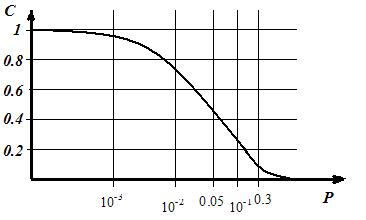
Рис. 1.7. Зависимость емкости «бинарного» канала с шумами от вероятности искажения сообщения Р.

Скорость передачи информации при воздействии шумов уменьшается более резко, чем число правильных принятых символов.

Выражение (3.16) как доказал Шеннон, показывает, что если энтропия источника информации не превышает пропускной способности канала, т.е. H≤C, то существует код, обеспечивающий передачу информации через канал с шумами со сколь угодно малой частотой ошибок.

При H>C такого кода не существует, т.е. невозможна передача без ошибок.

Полученный Шенноном результат представляет собой одну из основных теорем теории информации.

К. Шенноном же была определена пропускная способность или емкость канала связи при ограниченной средней мощности аналогового сигнала и равномерном спектре сигнала и помехи:

C=F_m log₂(1+W_c/W_ш) (3.17)

где: F- полоса частот канала;

W_c- средняя мощность сигнала;

W_ш- средняя мощность белого шума (с равномерным спектром) с нормальным законом распределения амплитуд в полосе частот канала связи.

Следовательно, можно передавать информацию по каналу с помехами без ошибок, если скорость передачи информации

R≤C=F_m log₂ (1+W_c/W_ш) (3.18)

Для R>C при любой системе кодирования частота ошибок конечна, при чем она быстро растет с увеличением R (скорости).

Из формулы (3.18) следует, что в канале с высоким уровнем шумов, т.е. при W_c<<W_ш емкость канала резко уменьшается. При малых W_c/W_ш выражение (3.18) можно разложить в ряд и ограничиться одним членом ряда (3.19)

C=F_m log ₂ (1+W_c/W_ш) = F_m log₂ (W_c/W_m)= 1,44 F_m (W_c/W_m) (3.19)

Из (3.19) следует, что емкость канала связи неограниченно возрастает с W_ш→0.

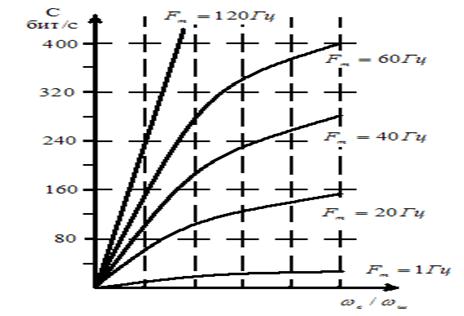Однако практически это невозможно из-за аппаратурных погрешностей и шумов, уменьшающих пропускную способность (емкость) канала.

На рис. 1.7 представлена зависимость пропускной способности канала для различных значений полосы частот канала.

Рис. 1.8

(назад в оглавление)

Дата добавления: 2014-01-06