Коды и кодирование. Оптимальный код Шеннона-Фано

Лекция 3

Для того чтобы увеличить скорость передачи до предельной пропускной способности канала необходимо статистически согласовать источник с каналом. Для этого между ними включают преобразователь.

x y

Рис. 1.9

Преобразователь называется кодером, реализующим закон преобразования (закон по которому исходный алфавит преобразуется в выходной) информации, т.е. чтобы выполнялось условие формулы (3.16)

Z=R=S [H_i-H_j(i)] (4.1)

Под кодированием в широком смысле слова подразумевается представление сообщений в форме, удобной для передачи по данному каналу.

Обратная операция называется декодированием.

Рис. 1.10.

Здесь:

ИИ - источник информации

КИ - кодер источника

КК - кодер канала

М - модулятор

ДМ - демодулятор

ДК - декодер канала

ДИ - декодер источника

П - приемник

Сообщению Z на выходе источника необходимо поставить в соответствие определенный сигнал. Поскольку число возможных сообщений при неограниченном увеличении времени стремится к бесконечности, а за достаточно большой промежуток времени весьма велико, то создать для каждого сообщения свой сигнал практически невозможно.

Поэтому, при большом объеме алфавита, часто прибегают к представлению букв одного (1-го) алфавита буквами другого (2-го) алфавита с меньшим числом букв. Это кодирование в узком смысле слова.

Т.о. каждой букве 1-го алфавита соответствует некоторая (некоторое сочетание) последовательность символов другого алфавита, называемая кодовой комбинацией. Число символов в кодовой комбинации называется ее значностью.

В своих основных теоремах Шеннон обосновал эффективность введения кодовых комбинаций в тракт кодирующих и декодирующих устройств. Преобразование одной кодовой последовательности в другую означает преобразование алфавита и самой информации так, чтобы выполнялось как условие (3.16), именно условие

I = H_max (4.2)

т.е. когда появление «0» и «1» равновероятно.

Бинарным Кодом называется конечное множество целых рациональных чисел, сопоставляемых по определенному алгоритму с множеством сообщений.

Код имеет следующие основные характеристики:

1. Основание кода m, равное числу отличающихся друг от друга символов в алфавите (называемых также буквами в алфавите).

Простейший код = число – импульсный состоит из одних единиц. Так при дискретизации значение какого-либо параметра может быть представлено определенным числом (число – импульсных единиц).

Все другие коды имеют алфавит из двух (m=2 – двоичные коды) и более символов (например, алфавит русского языка –33 символа), природа же, например, пользуется при записи информации в ДНК четырех буквенным алфавитом m = 4.

2. Длина кодовой комбинации n, называемая также разрядностью кода или длиной слова; n равно числу одинаковых или отличающихся друг от друга символов (элементарных сигналов) в кодовой комбинации. Для данного кода характерно свое множество (набор) кодовых комбинаций, каждая из которых может передавать отдельное дискретное сообщение. Код называется равномерным, если все кодовые комбинации одинаковы по длине (n=const) и неравномерным, если величина n в коде непостоянна (n=var).

3. Число кодовых комбинаций N в коде, каждая из которых может передавать свое отдельное сообщение, N называется также объемом кода.

Код удобно представить в виде матрицы K_n,N, имеющий N строк и n столбцов, где K может принимать значения от 0 до m-1:

(4.3)

Каждая строка матрицы представляет собой кодовую комбинацию, и если длина каждой строки постоянна (n=const), то код будет равномерным.

Число строк в матрице равно числу кодовых комбинаций N. Код называется полным, если N=n^m. Так для простейшего кода m=1 и N=n_max, это неравномерный код. Во всех других кодах N>n.

Кроме того, есть характеристики кода, которые зависят от способа передачи и отображения. Так, по характеру передачи кодовых комбинаций они делятся, на параллельный и последовательный способы передачи отдельных символов (соответственно и коды упрощенно называют параллельным и последовательным кодом).

Рассмотрим простейший пример:

Пусть имеется источник сообщений, который передает в канал сообщение в виде последовательности символов, взятых из некоторого алфавита m = 4:

α; β; γ; Δ (4.4)

И пусть последовательность сообщений имеет вид:

α β α γ α β α γ α Δ α β α γ α β γ α γ α β α Δ α β α γ α β α (4.5)

т.е. длина n=30, тогда вероятности распределятся следующим образом:

P(α) ≈ 15/30=0.5

P(β) ≈ 7/30=0.23(3) (4.6)

P(γ) ≈ 6/30=0.2

P(Δ) ≈ 2/30=1/15=0.06(6)

Тогда энтропия источника определяется:

Н_ист= -PαlogPα - PβlogPβ - PγlogPγ - PΔlogPΔ = -15/30log15/30 - 7/30log7/30 - 6/30log6/30 -2/30log2/30 ≈ 0.83 (бит).

Т.е.

Н_ист=0,83<H_max= log₂4 =2 бит

Т.о. исходное сообщение имеет малую энтропию, и передача будет не эффективной, т.к. имеется излишняя избыточность.

Для этого необходимо преобразовать исходный алфавит в новый скажем двоичный и тогда:

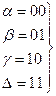(4.8)

т.е. мы преобразовали в алфавит m=2 и n=2 и тогда сообщение (4.5) станет

00 01 00 10 00 01 00 10 00 11 00 01 00 10 00 01 10 00 10 00 01 00 11 00 01 00 10 00 01 00

α β α γ α β α γ α Δ α β α γ α β γ α γ α

β α Δ α β α γ α β α (4.9)

Здесь N₂ = 60 и тогда вероятности появления «0» и «1» будут:

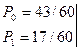(4.10)

И новая энтропия источника:

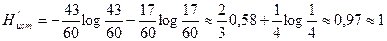(бит) (4.11)

Т.о. преобразовав исходное сообщение в равномерный код, нам удалось повысить энтропию.

Попробуем теперь неравномерный код. Для этого присвоим:

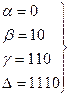(теперь n=var) (4.12)

Тогда N₃ возрастет до 55 по сравнению с исходным (4.5) (N=30).

И из примера видно, что неравномерный код короче равномерного (N₂>N₃).

Дата добавления: 2014-01-06