Кодовое расстояние

Степень отличия любых двух кодовых комбинаций характеризуется расстоянием между ними в смысле Хемминга или просто кодовым расстоянием. Оно выражается числом символов, в которых кодовые комбинации отличаются одна от другой, и обозначается через d.

Чтобы получить кодовое расстояние между двумя какими-либо комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2. Например:

d=7

Так определим кодовое расстояние в коде Грея:

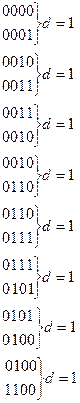здесь d=const t=1

N₁₀ N₂ d₂ N_гр d_гр

В коде Грея все кодовые комбинации информационные, минимальное кодовое расстояние d_min = 1. Такие коды называются беизбыточными.

Как мы отмечали ранее, количество информации в бинарном алфавите определится числом возможных комбинаций «0» и «1», т.е. числом размещений из n элементов с повторениями по l.

M=I=2^l (т.к. n = 2) (4.29)

Как уже отмечалось такие коды не помехоустойчивые и, следовательно, для увеличения помехоустойчивости кода необходимо ввести избыточность (ввести дополнительный символ).

Пусть имеется некоторое сообщение, состоящее из n символов двоичного кода (последовательность «0» и «1»), тогда количество единиц равно m, количество нулей равно n-m. Добавим к n – мерной последовательности n + 1 символ такой («0» или «1»), чтобы количество «1» (единиц) стало четным

(1+m)=2k (k<m<n)

Т.о. создается признак, по которому можно судить об искажениях в процессе передачи, обусловленный наличием избыточных символов.

Код не обнаруживает искажений четного числа символов. Такой код называется кодом Хемминга.

В общем случае, число избыточных символов может быть больше одного (т.е. k).

Тогда из 2ⁿ различных входных комбинаций образуется 2^n+k различных выходных последовательностей.

Назовем число 2ⁿ комбинаций разрешенными, тогда

2^n+k =2ⁿ – запрещенныекодовыекомбинации.

Искажение информации сводится к тому, что каждая из 2ⁿ разрешенных кодовых комбинаций может трансформироваться в любую другую, то есть всего имеется возможных случаев передачи.

При этом имеем:

2ⁿ –случаев безошибочной передачи;

2ⁿ (2ⁿ -1) –случаев перехода в другие разрешенные комбинации (случай необнаруживаемых ошибок);

2ⁿ (2^n+k -2ⁿ) – случаев перехода в неразрешенные комбинации (случай опознаваемых ошибок).

Следовательно, число опознанных ошибок от общего числа возможных случаев передачи составит:

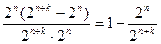(4.30)

Так для кода Хемминга, рассмотренного ниже, имеем

(4.31)

Т.о. на приемной стороне легко будет выявляться пришла разрешенная или неразрешенная комбинация, более того по типу неразрешенной комбинации можно восстановить исходную разрешенную комбинацию. При этом отношение числа исправленных кодом ошибок к числу обнаруживаемых определяется соотношением

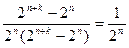(4.32)

Большинство разработанных до недавнего времени кодов предназначено для корректирования (обнаружения и исправления) взаимно независимых ошибок определенной кратности и пачек ошибок. Взаимно независимые это такие ошибки в передаваемой последовательности, для которых вероятность появления ошибочной комбинации зависит только от числа искаженных символов r и вероятности искажения одного символа p.

(назад в оглавление)

Дата добавления: 2014-01-06