
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Редактор Paint
|
|
|
|
ГРАФИЧЕСКИЕ РЕДАКТОР PAINT
Создать объекты иллюстративной графики, включая динамические ролики, можно средствами программирования, а также графическими редакторами и системами. Рассмотрим два из них.
Графический редактор Paint, входящий в комплект стандартных программ MS Windows 95/98/Me/2000/XP, позволяет, используя манипулятор «мышь», выполнять черно-белые и цветные рисунки, обрамлять их текстом, выводить на печать. В Paint можно работать с фрагментами графических изображений: копировать, перемещать, поворачивать, изменять размеры, записывать на диск и считывать с диска. С помощью Paint можно обрабатывать графические изображения, а также считывать и записывать в файл полностью или частично изображение с дисплея, если монитор работает в графическом режиме.
После загрузки пакета появляется рабочий экран редактора. Большую часть экрана занимает рабочее поле, окрашенное в фоновый цвет. Над рабочим полем – меню, позволяющее выполнять команды редактирования. Слева от рабочего поля расположена панель инструментов, на которой высвечен инструмент, в данный момент являющийся рабочим. Под рабочим полем находится палитра. С левого края палитры показаны два вложенных квадрата, внутренний из которых окрашен в рабочий цвет, а внешний – в фоновый. В левом нижнем углу экрана выводится калибровочная шкала, которая позволяет устанавливать ширину рабочего инструмента (кисти, резинки и т.д.). Установленная в данный момент ширина инструмента отмечена стрелкой. Вдоль нижнего правого и правого края рабочего поля находятся линейки прокрутки для перемещения рабочего поля по картинке, если размеры картинки больше размеров рабочего поля.
Общие правила работы с редактором таковы. Для выбора (установки) параметров работы и выполнения команд в Paintbrush необходимо поместить указатель мыши на пункт меню и щелкнуть левой кнопкой. Выход из программы File/Quit.
4. Алгоритмизация и программирование – 4 часа.
Понятие алгоритма: свойства алгоритмов, исполнители алгоритмов, система команд исполнителя. Способы записей алгоритмов. Основные алгоритмические конструкции. Вспомогательные алгоритмы. Процесс создания и отладки программ.
5.1. Алгоритмизация
Понятие алгоритма: свойства, исполнители, СКИ. Способы записей алгоритмов. Основные алгоритмические конструкции. Вспомогательные алгоритмы. Процесс создания и отладки алгоритма. Примеры типовых алгоритмов.
1. Запись программы на метаязыке. Метаязык — это любой способ описания последовательности действий, понятный людям. Когда человеку, заблудившемуся в незнакомом городе, объясняют, как куда-то пройти, фактически ему дают программу действий на метаязыке.
Алгоритм — это формальное описание способа решения задачи путем разбиения ее на последовательность элементарных операций. Слово «формальное» означает, что описание должно быть абсолютно полным и учитывать все возможные ситуации, которые могут возникнуть по ходу решения. Понятие алгоритма - одно из фундаментальных понятий информатики. Алгоритмизация наряду с моделированием выступает в качестве общего метода информатики. К реализации определенных алгоритмов сводятся процессы управления в различных системах, что делает понятие алгоритма близким и кибернетике. Алгоритмы являются объектом систематического исследования пограничной между математикой и информатикой научной дисциплины, примыкающей к математической логике - теории алгоритмов. Особенность положения состоит в том, что при решении практических задач, предполагающих разработку алгоритмов для реализации на ЭВМ, и тем более при использовании на практике информационных технологий, можно, как правило, не опираться на высокую формализацию данного понятия. Поэтому представляется целесообразным познакомиться с алгоритмами и алгоритмизацией на основе содержательного толкования сущности понятия алгоритма и рассмотрения основных его свойств. При таком подходе алгоритмизация выступает как набор определенных практических приемов, особых специфических навыков рационального мышления в рамках заданных языковых средств. Само слово «алгоритм» происходит от algorithm - латинской формы написания имени великого математика IX века Мухаммеда аль-Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмами и понимали только правила выполнения четырех арифметических действий над многозначными числами. Понятие исполнителя невозможно определить с помощью какой-либо формализации. Исполнителем может быть человек, группа людей, робот, станок, компьютер, язык программирования и т.д. Важнейшим свойством, характеризующим любого из этих исполнителей, является то, что исполнитель умеет выполнять некоторые команды. Вся совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя (СКИ). Одно из принципиальных обстоятельств состоит в том, что исполнитель не вникает в смысл того, что он делает, но получает необходимый результат. В таком случае говорят, что исполнитель действует формально, т.е. отвлекается от содержания поставленной задачи и только строго выполняет некоторые правила, инструкции. Это важная особенность алгоритмов. Наличие алгоритма формализует процесс решения задачи, исключает рассуждение исполнителя. Использование алгоритма дает возможность решать задачу формально, механически исполняя команды алгоритма в указанной последовательности. Целесообразность предусматриваемых алгоритмом действий обеспечивается точным анализом со стороны того, кто составляет этот алгоритм. Введение в рассмотрение понятия «исполнитель» позволяет определить алгоритм как понятное и точное предписание исполнителю совершить последовательность действий, направленных па достижение поставленной цели. Наиболее распространенными и привычными являются алгоритмы работы с величинами - числовыми, символьными, логическими и т.д. Алгоритм, составленный для некоторого исполнителя, можно представить различными способами: с помощью графического или словесного описания, в виде таблицы, последовательностью формул, записанным на алгоритмическом языке (языке программирования). Остановимся на графическом описании алгоритма, называемом блок-схемой. Этот способ имеет ряд преимуществ благодаря наглядности, обеспечивающей, в частности, высокую «читаемость» алгоритма и явное отображение управления в нем. Прежде всего, определим понятие блок-схемы. Блок-схема - это ориентированный граф, указывающий порядок исполнения команд алгоритма; вершины такого графа могут быть одного из трех типов (рис. 1).
 Рис. 1. Три типа вершин графа
Рис. 1. Три типа вершин графа
На рис. 1 изображены «функциональная» (а) вершина (имеющая один вход и один выход); «предикатная» (б) вершина, имеющая один вход и два выхода (в этом случае функция Р передает управление по одной из ветвей в зависимости от значения Р (Т, т.е. true, означает «истина», F, т.е. false - «ложь»); «объединяющая» (в) вершина (вершина «слияния»), обеспечивающая передачу управления от одного из двух входов к выходу. Иногда вместо Т пишут «да» (либо знак +), вместо F - «нет» (либо знак -).
Из данных элементарных блок-схем можно построить четыре блок-схемы (рис. 2), имеющих особое значение для практики алгоритмизации.

Рис. 2. Основные алгоритмические структуры
На рис. 2 изображены следующие блок-схемы: а - композиция, или следование; б - альтернатива, или развилка, в и г - блок-схемы, каждую из которых называют итерацией, или циклом (с предусловием (в), с постусловием (г)). S1 и S2 представляют собой в общем случае некоторые серии команд для соответствующего исполнителя, Б — это условие, в зависимости от истинности (Т) или ложности (F) которого управление передаётся по одной из двух ветвей. Можно доказать, что для составления любого алгоритма достаточно представленных выше четырех блок-схем, если пользоваться их последовательностями и/или суперпозициями. Блок-схема «альтернатива» может иметь и сокращенную форму, в которой отсутствует ветвь S2 (рис.3, а). Развитием блок-схемы типа альтернатива является блок-схема «выбор» (рис.3, б).

Рис. 3. Развитие структуры типа «альтернатива»: а) - неполная развилка; б) ~ структура «выбор»
На практике при составлении блок-схем оказывается удобным использовать и другие графические знаки (некоторые из них приведены на рис.4).
Рис. 4. Некоторые дополнительные конструкции для изображения блок-схем алгоритмов
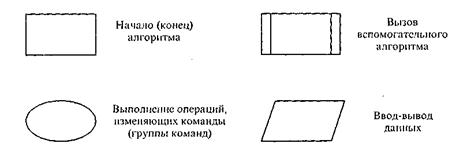 Алгоритм должен быть составлен таким образом, чтобы исполнитель мог однозначно и точно следовать командам алгоритма и эффективно получать определенный результат. Это накладывает на записи алгоритмов ряд обязательных требований, суть которых вытекает из неформального толкования понятия алгоритма. Сформулируем эти требования в виде перечня свойств, которым должны удовлетворять алгоритмы, адресуемые заданному исполнителю.
Алгоритм должен быть составлен таким образом, чтобы исполнитель мог однозначно и точно следовать командам алгоритма и эффективно получать определенный результат. Это накладывает на записи алгоритмов ряд обязательных требований, суть которых вытекает из неформального толкования понятия алгоритма. Сформулируем эти требования в виде перечня свойств, которым должны удовлетворять алгоритмы, адресуемые заданному исполнителю.
1.Одно из первых требований, которое предъявляется к алгоритму, состоит в том, что описываемый процесс должен быть разбит на последовательность отдельных шагов. Возникающая в результате такого разбиения запись представляет собой упорядоченную совокупность четко разделенных друг от друга предписаний (директив, команд, операторов), образующих прерывную (или, как говорят, дискретную) структуру алгоритма. Только выполнив требования одного предписания, можно приступить к выполнению следующего. Дискретная структура алгоритмической записи может, например, подчеркиваться сквозной нумерацией отдельных команд алгоритма, хотя это требование не является обязательным. Рассмотренное свойство алгоритмов называют дискретностью.
2. Используемые на практике алгоритмы составляются с ориентацией на определенного исполнителя. Чтобы составить для него алгоритм, нужно знать, какие команды этот исполнитель может понять и исполнить, а какие - не может. Составляя запись алгоритма для определенного исполнителя, можно использовать лишь те команды, которые имеются в его СКИ. Это свойство алгоритмов будем называть понятностью.
3. Будучи понятным, алгоритм не должен содержать предписаний, смысл которых может восприниматься неоднозначно, т.е. одна и та же команда, будучи понятна разным исполнителям, после исполнения каждым из них должна давать одинаковый результат. Запись алгоритма должна быть настолько четкой, полной и продуманной в деталях, чтобы у исполнителя не могло возникнуть потребности в принятии решений, не предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять места для произвола исполнителя. Кроме того, в алгоритмах недопустимы также ситуации, когда после выполнения очередной команды алгоритма исполнителю неясно, какая из команд алгоритма должна выполняться на следующем шаге. Отмеченное свойство алгоритмов называют определенностью или детерминированностью.
4. Обязательное требование к алгоритмам - результативность. Смысл этого требования состоит в том, что при точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен получиться определенный результат. Вывод о том, что решения не существует – тоже результат.
5. Наиболее распространены алгоритмы, обеспечивающие решение не одной конкретной задачи, а некоторого класса задач данного типа. Это свойство алгоритма называют массовостью. В простейшем случае массовость обеспечивает возможность использования различных исходных данных.
Достаточно распространенным способом представления алгоритма является его запись на алгоритмическом языке, представляющем в общем случае систему обозначений и правил для единообразной и точной записи алгоритмов и исполнения их. Отметим, что между понятиями «алгоритмический язык» и «языки программирования» есть различие; прежде всего, под исполнителем в алгоритмическом языке может подразумеваться не только компьютер, но и устройство для работы «в обстановке». Программа, записанная на алгоритмическом языке, не обязательно предназначена компьютеру. Практическая же реализация алгоритмического языка - отдельный вопрос в каждом конкретном случае. Как и каждый язык, алгоритмический язык имеет свой словарь. Основу этого словаря составляют слова, употребляемые для записи команд, входящих в систему команд исполнителя того или иного алгоритма. Такие команды называют простыми командами. В алгоритмическом языке используют слова, смысл и способ употребления которых задан раз и навсегда. Эти слова называют служебными. Использование служебных слов делает запись алгоритма более наглядной, а форму представления различных алгоритмов - единообразной. Алгоритм, записанный на алгоритмическом языке, должен иметь название. Название желательно выбирать так, чтобы было ясно, решение какой задачи описывает данный алгоритм. Для выделения названия алгоритма перед ним записывают служебное слово АЛГ (АЛГоритм). За названием алгоритма (обычно с новой строки) записывают его команды. Для указания начала и конца алгоритма его команды заключают в пару служебных слов НАЧ (НАЧало) и КОН (КОНсц). Команды записывают последовательно.
Последовательность записи алгоритма:
АЛГ название алгоритма
НАЧ
серия команд алгоритма
КОН
При построении новых алгоритмов могут использоваться алгоритмы, составленные ранее. Алгоритмы, целиком используемые в составе других алгоритмов, называют вспомогательными алгоритмами. Вспомогательным может оказаться любой алгоритм из числа ранее составленных. Не исключается также, что вспомогательным в определенной ситуации может оказаться алгоритм, сам содержащий ссылку на вспомогательные алгоритмы. Очень часто при составлении алгоритмов возникает необходимость использования в качестве вспомогательного одного и того же алгоритма, который к тому же может быть весьма сложным и громоздким. Было бы нерационально, начиная работу, каждый раз заново составлять и запоминать такой алгоритм для его последующего использования. Поэтому в практике широко используют, так называемые, встроенные (или стандартные) вспомогательные алгоритмы, т.е. такие алгоритмы, которые постоянно имеются в распоряжении исполнителя. Обращение к таким алгоритмам осуществляется так же, как и к «обычным» вспомогательным алгоритмам. Алгоритм может содержать обращение к самому себе как вспомогательному и в этом случае его называют рекурсивным. Если команда обращения алгоритма к самому себе находится в самом алгоритме, то такую рекурсию называют прямой. Возможны случаи, когда рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение. Такая рекурсия называется косвенной. Пример прямой рекурсии:
АЛГ движение
НАЧ
вперед
вперед
вправо
движение
КОН
Алгоритмы, при исполнении которых порядок следования команд определяется в зависимости от результатов проверки некоторых условий, называют разветвляющимися. Для их описания в алгоритмическом языке используют специальную составную команду - команда ветвления. Она соответствует блок-схеме «альтернатива» и также может иметь полную или сокращенную форму.
ЕСЛИ условие ЕСЛИ условие ЕСЛИ край
ТО серия1 ТО серия ТО вправо
ИНАЧЕ серия2 ВСЕ ИНАЧЕ вперед
ВСЕ ВСЕ
Ниже приводится запись на алгоритмическом языке команды выбора (см. рис.3, б), являющейся развитием команды ветвления:
ВЫБОР
ПРИ условие 1: серия 1
ПРИ условие 2: серия 2
..........
ПРИ условие N: серия N
ИНАЧЕ серия N+1
ВСЕ
Алгоритмы, при исполнении которых отдельные команды или серии команд выполняются неоднократно, называют циклическими. Для организации циклических алгоритмов в алгоритмическом языке используют специальную составную команду цикла. Она соответствует блок-схемам типа «итерация» и может принимать следующий вид:
ПОКА условие НЦ
НЦ серия
серия ДО условие
КЦ КЦ
В случае составления алгоритмов работы с величинами можно рассмотреть и другие возможные алгоритмические конструкции, например, цикл с параметром или выбор. Подробно эти конструкции будут рассматриваться при знакомстве с реальными языками программирования. Понятие алгоритма, рассмотренное выше, можно назвать понятием алгоритма в интуитивном смысле. Оно имеет нечеткий, неформальный характер, ссылается на некоторые точно не определенные, но интуитивно понятные вещи. Например, при определении и обсуждении свойств алгоритма мы исходили из возможностей некоторого исполнителя алгоритма. Его наличие предполагалось, но ничего определенного о нем не было известно. Говоря языком математики, ни аксиоматического, ни исчерпывающего конструктивного определения исполнителя мы так и не дали. Установленные свойства алгоритмов следует называть эмпирическими. Они выявлены на основе обобщения свойств алгоритмов различной природы и имеют прикладной характер. Этих свойств достаточно для практического программирования, для создания обширного круга программ для компьютеров, промышленных роботов и т.д. Однако, как фундаментальное научное понятие алгоритм требует более обстоятельного изучения. Оно невозможно без уточнения понятия «алгоритм», более строгого его описания или, как еще говорят, без его формализации.
Известно несколько подходов к формализации понятия «алгоритм»:
· теория конечных и бесконечных автоматов;
· теория вычислимых (рекурсивных) функций;
· λ -исчисление Черча.
Все эти возникшие исторически независимо друг от друга подходы оказались впоследствии эквивалентными. Главная цель формализации понятия алгоритма такова: подойти к решению проблемы алгоритмической разрешимости различных математических задач, т.е. ответить на вопрос, может ли быть построен алгоритм, приводящий к решению задачи. Формализацию понятия алгоритма можно рассмотреть в теории автоматов на примере машин Поста, Тьюринга, а также нормальных алгоритмов Маркова. Идеи λ-исчислений Черча реализованы в языке программирования LISP. Вместе с тем, формально определенный любым из известных способов алгоритм не может в практическом программировании заменить то, что мы называли алгоритмами. Основная причина состоит в том, что формальное определение резко сужает круг рассматриваемых задач, делая многие практически важные задачи недоступными для рассмотрения.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1176; Нарушение авторских прав?; Мы поможем в написании вашей работы!