Абстрактные алгоритмические машины

Абстрактные (т.е. существующие не реально, а лишь в воображении) машины Поста и Тьюринга, предназначенные для доказательств различных утверждений о свойствах программ для них, были предложены независимо друг от друга (и прак­тически одновременно) в 1936 г. американским математиком Эмилем Постом и английским математиком Аланом Тьюрингом. Эти машины представляют собой универсальных исполнителей, являющихся полностью детерминированными, позволяющих «вводить» начальные данные, и после выполнения программ «читать» результат. 1) МАШИНА ПОСТА. Абстрактная машина Поста представляет собой бесконечную ленту, разделен­ную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V», и головку, которая может перемещаться вдоль ленты на одну клетку вправо или влево, заносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, или проверять наличие метки в клетке. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый

момент времени головка («-») находится над одной из клеток ленты и, как говорят, обозре­вает ее. Информация о местоположения головки вместе с состоянием ленты харак­теризует состояние машины Поста. Команды машины Поста имеют следующую структуру: nKm, где n - порядковый номер команды, K – действие, выполняемое головкой, m – номер следующей команды, подлежащей выполнению. Существует 6 команд машины Поста: движение головки на одну клетку вправо, на одну клетку влево, перенесение метки в клетку, над которой находится головка, стирание метки из клетки, проверка наличия метки, остановка машины. 2) МАШИНА ТЬЮРИНГА. Машина Тьюринга состоит из счетной ленты (разделенной на ячейки, ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжного механизма и исполнительного операционного устройства, которое может находиться в одном из дискретных состояний q₀, q₁,…q_s, принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний). Читающая и пишущая головка может читать буквы рабочего алфавита A={a₀, a₁,…a_t}, стирать и печатать их. Порядок работы МТ описывается таблицей машины Тьюринга. Эта таблица является матрицей с четырьмя столбцами и (s+1)(t+1) строками. Каждая строка имеет вид:

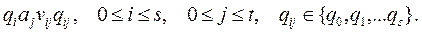
Здесь через v_ij обозначен элемент объединения алфавита и множества предписаний для лентопротяжного механизма: l(Л) – переместить ленту влево, r(П) – переместить ленту вправо, s(С) – остановить машину; v_ij – действие МТ, состоящее либо в занесении в ячейку ленты символа алфавита, либо в движении головки, либо в остановке машины; q_ij является последующим состоянием.

Пример 1. Алгоритм прибавления единицы к числу n в десятичной системе счисления. Дана десятичная запись числа n. Требуется получить десятичную запись числа n =1. Внешний алфавит МТ: 0,1,2,3,4,5,6,7,8,9,_. Эти цифры записываются в одной ячейке подряд, без пропусков. Внутреннее состояние q₁: движение головки к цифре единиц числа Внутреннее состояние q₂: замена этой цифры на единицу большую Схема МТ:

ai	qi
Q1	Q2
	0Пq1	1Cq2
	1Пq1	2Cq2
	2Пq1	3Cq2
	3Пq1	4Cq2
	4Пq1	5Cq2
	5Пq1	6Cq2
	6Пq1	7Cq2
	7Пq1	8Cq2
	8Пq1	9Cq2
	9Пq1	0Cq2
-	-Лq1	1Cq2

3) НОРМАЛЬНЫЕ АЛГОРИТМЫ МАРКОВА. Для формализации понятия алгоритма российский математик А.А.Марков предложил использовать ассоциативные исчисления. Пусть имеется алфавит А. Составляющие его символы называют буквами. Конечная последовательность букв алфавита называется словом в этом алфавите. Совокупность всех слов в данном алфавите вместе с системой допустимых подстановок называют ассоциативным исчислением. (подстановка N-M допустима к некоторому слову К: если в К имеется одно или несколько вхождений слова N, то любое из них может быть заменено словом M, и наоборот, если имеется вхождение M, то его можно заменить словом N) Алгоритмом в алфавите А называется понятное точное предписание, определяющее процесс над словами из А и допускающее любое слово в качестве исходного. Алгоритм задается в виде системы допустимых подстановок, дополненной точным предписанием о том, в каком порядке нужно применять допустимые подстановки и когда наступает остановка.

Пример1. Алфавит: А={a,b,c} Система подстановок В: cb – cc, cca – ab, ab – bca. Предписание о применении подстановок: в произвольном слове P надо сделать возможные подстановки, заменив левую часть подстановок на правую; повторить процесс с вновь полученным словом. Так, применяя систему подстановок В из рассмотренного примера к словам babaac и bcacabc получаем:

babaac→bbcaaac→остановка

bcacabc→bcacbcac→bcacccac→bcacabc→бесконечный процесс(т.к. получили исходное слово).

Предложенный Марковым способ уточнения понятия алгоритма основан на понятии нормального алгоритма, который определяется следующим образом. Пусть задан алфавит А и система подстановок В. Для произвольного слова P подстановки из В подбираются в том же порядке, в каком они следуют в В. Если подходящей подстановки нет, то процесс останавливается. В противном случае берется первая из подходящих подстановок и производится замена ее правой частью первого вхождения ее левой части в P. Затем все действия повторяются для получившегося слова P₁. Если применяется последняя подстановка из системы В, процесс останавливается. Такой набор предписаний вместе с алфавитом А и набором подстановок В определяют нормальный алгоритм.

Дата добавления: 2014-01-06