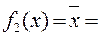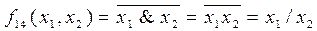Переключательные функции одного и двух переменных

.

Рассмотрим некоторые ПФ одного и двух аргументов. В табл. 2.2 представлены все 4 функции одного аргумента.

Таблица 2.2

x	f0(x)	f1(x)	f2(x)	f3(x)

Функция f₀ (x) равно нулю (константа нуля), f₃(x) равна единице (константа единицы), функция f₁(x) повторяет значение аргумента, т.е. f₁(x)=x. Наиболее интересной и имеющей важное значение является функция f₂(x), которая принимает значения, обратные значению аргумента – логическое отрицание или функция НЕ и обозначается как:

ù х (читается не х).

Все ПФ двух аргументов приведены в табл.2.3.

Таблица 2.3

х1

х2

f0

f1

f2

f3

f4

f5

f6

f7

f8

f9

f10

f11

f12

f13

f14

f15

Функции f₀(x₁,x₂) и f₁₅(x₁,x₂) не зависят от значений аргументов: f₀(x₁,x₂)=0 и f₁₅(x₁,x₂)=1. Функции f₃(x₁,x₂), f₅(x_1, x₂), f₁₀(x₁,x₂) и f₁₂(x₁,x₂) являются фактически функциями одного аргумента:

f₃(x₁,x₂)=x₁, f₅(x₁,x₂)=x₂, f₁₀(x₁,x₂)=x₂ и f₁₂(x₁,x₂)=x₁.

Рассмотрим часто встречающиеся ПФ. Функция f₁(x₁,x₂) реализует операцию конъюнкции или логического произведения. Как видим из табл.2.3, функция f₁(x₁,x₂) равна 1, когда и x₁ и x₂ равны 1. Конъюнкция обозначается как

f₁(x₁,x₂)=x₁ & x₂ = x₁ Ù x₂ = x₁ x₂ (читается x₁ и x₂).

Функция f₇(x₁,x₂) реализует операцию дизъюнкцию или логического сложения. Функция равна 1, когда или x₁ или x₂ равны 1. Дизъюнкция обозначается как

f₇(x₁,x₂)=x₁ Ú x₂.

Функция f₁₄(x₁,x₂) реализует операцию отрицания конъюнкции. Из табл.2.3 видно, что когда конъюнкция f₁(x₁,x₁) равна 0, то функция f₁₄(x₁,x₂) равна 1, а если f₁(x_1, x₂) равна1, то f₁₄(x₁,x₂) равна 0, т.е. f₁₄(x₁,x₂)=f₁(x₁,x₂). Эта операция получила название “штрих Шеффера” и обозначается различными способами:

Функция f₈(x₁, x₂) реализует операцию отрицания дизъюнкции. По аналогии с функцией отрицания конъюнкции, из табл.2.3 видно, что f₈(x₁, x₂)=f₇(x₁, x₂). Эта операция также получила отдельное название – “стрелка Пирса” и обозначается следующим образом:

Функция f₆(x₁, x₂) реализует операцию логической неравнозначности или еще ее называют суммой по модулю два. ПФ равна 1, если аргументы x₁ и x₂ не равны между собой.

Остальные ПФ двух аргументов рассматривать не будем. В действительности, для реализации сколь угодно сложной ПФ не обязательно использовать все 16 ПФ двух аргументов. Можно ограничиться некоторым набором, с помощью которого можно строить любые ПФ.

Система ПФ, из которых с помощью операций суперпозиции и подстановки можно получить любую сколь угодно сложную ПФ, называется функционально полной системой переключательных функций (ФПС ПФ). Существует несколько ФПС ПФ:

- дизъюнкция, конъюнкция и отрицание;

- отрицание конъюнкции;

- отрицание дизъюнкции и другие.

Возникает вопрос, какие ФПС ПФ представляют наибольший практический интерес? Выбор ФПС ПФ с технической точки зрения эквивалентен выбору типов логических элементов, из которых может быть построена любая логическая схема. Оказывается, что наиболее удобной для решения задач синтеза схемы является ФПС ПФ, содержащая дизъюнкцию, конъюнкцию и отрицание.

Дата добавления: 2014-01-06