Операции над соответствиями

В инженерной практике наиболее часто применяют следующие операции над соответствиями:

• теоретико-множественные
• инволюции (обращения)
• композиции (произведения, суперпозиции).

1) Теоретико-множественные операции над соответствиями С.

Поскольку С являются подмножествами множества, то можно говорить об объединении однотипных соответствий, их пересечении, разности и дополнении:

C1 È C2Í M1 * M2,

C1 Ç C2Í M1 * M2,

C1 / C2Í M1 * M2,

C=(M1 * M2)/C

Замечание. Соответствия и булевы операции над ними {È,Ç,- }образуют булеву алгебру ‹B (M1 * M2),È,Ç,- ›, где несущим множеством является булеан декартова произведения.

2) Инволюция соответствия.

Инволюцией q^-1 = ‹M₂, M₁,S^-1 › соответствия q=‹M₁,M₂,S › называется множество: S^-1 {‹y,x› M₂*M₁: ‹x,y› S}

Из этого определения следует, что S^-1 является обратным к S

Пример. Пусть

Тогда:

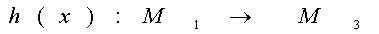
И им соответствуют графы:

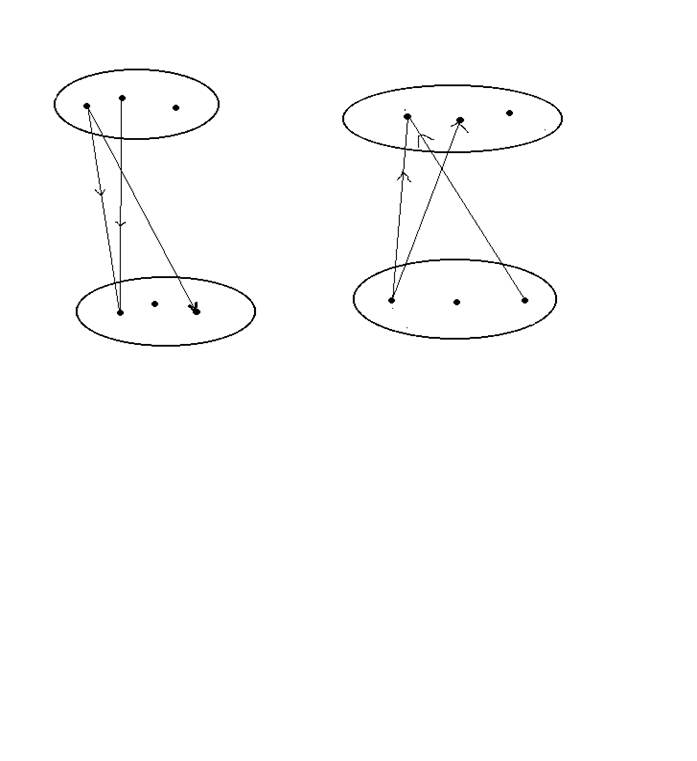
3 ) Композиция соответствия. Композиция есть бинарная операция с тремя множествами, такими, что соответствия есть q₁ и q₂, где q₁ = ‹M₁, M ₂,S₁ ›, q₂ = ‹M₂, M ₃, S₂›

Пр_m2S =Пр_m2S₂

q₁*q₂ = ‹ M₁, M₃, S₁*S₂ ›

q₁ = ‹M₁, M₂, S ₁› q₂ = ‹ M₂, M₃, S₂›

Примечание. 1) Свойства операций композиции над соответствиями:

1. (S_1*S₂)_*S₃ = S_1*(S_2*S₃) – ассоциативность

2. Дистрибутивность:

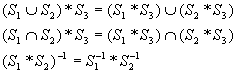
2) В общем случае операция * некоммутативна: S_1*S₂ S_{2 *}S₁

3) Запись h(x) = g(f(x)) означает композицию двух функциональных отображений вида:

и 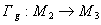. В этом случае и говорят, что h(x) получено подстановкой f в g.

Бинарные отношения.

Def 14. Бинарным отношением R во множестве M называется подмножество его квадрата M², т.е. R Í M².

Рассмотрим основные свойства отношений.

• Говорят, что х, у Î M находятся в отношении R, если ‹х, у› Î R (часто пишут и так хRу, т.е. ‹х,у› ~ хRу).
• Реляционная система ‹M, R› называется бинарным графом, где M – множество вершин (носитель графа), R – множество дуг (сигнатура графа).
• Отношение R во множестве M называется рефлексивным, если для каждого элемента х Î M справедливо, что ‹x, x› Î R. (свойство рефлекcивности при задании отношения R матрицей характеризуется тем, что все элементы главной диагонали являются 1; если R задано графом, то все его вершины имеют петли)
• Отношение R во множестве м называется симметричным, если из ‹x,y› Î R следует ‹y,x› Î R (х¹ y). Симметричное отношение представляет неограф, а его матрица симметрична относительно главной диагонали.
• Отношение R во множестве M называется транзитивным, если из ‹x,y› Î R и ‹x,z› Î R следует ‹x,z› Î R; x, y, z Î M, x ¹ y, x ¹ z, y ¹ z.

В графе ‹M, R›, задающем транзитивное отношение R Î M², для всякой пары дуг таких, что конец первой совпадает с началом второй, существует третья дуга, имеющая общее начало с первой и общий конец со второй (эту дугу называют транзитивно замыкающей дугой).

Пример. Пусть R = {‹x, y› Î N²: x,y Î N, х делитель у}.

Это отношение на множестве натуральных чисел:

• Рефлексивно, т.к. х/х = 1,
• Несимметрично, т.к. если 2 делитель 4, то 4 не является делителем 2
• Транзитивно, т.к. если у/х Î и z/у Î n, то z/x = у/х ´ z/у Î N.
• Антисимметрично, т.е. " х " у (хRу и уRx ® х=у), поскольку если х/у Î N и у/х Î N, то х=у.

Пример. Отношение упорядоченности £ рефлексивно, антисимметрично и транзитивно.

Пример. Отношение включения Ì есть отношение упорядоченности подмножеств заданного множества. Действительно, оно рефлексивно, т.к. M_i Ì M_i; антисимметрично, т.к. если M_i Ì M_j и M_j Ì M_i, то M_i = M_j; транзитивно, т.к. если M_i Ì M_j, M_{j Ì} M_k, to M_i Ì M_k.

Пример. Отношение "на 5 меньше, чем …" на множестве N является интранзитивным, т.к. если х=10, у=15, z=20, то х меньше у на 5, но х меньше z на 10, а не на 5.

Дата добавления: 2014-01-06