I) Группоиды (оперативы)

I. Группоиды ‹M,f2›.

f^2,e,b	Наличие свойств мультипликотивности для f^2	Наличие выделенных элементов в М для операции f^2
Название группоида	Ассоциативность f^2	Комутативность f^2	e	b
Полугруппа (ассоциат.группоид)	+
Моноид	+		+
Абелев моноид (абелева полугруппа с нейтрал. элементами)	+	+	+
Группа	+		+	+
Лупа			+	+
Абелева(комутатив.группа)	+	+	+	+

f^2,e,b	Наличие свойств мультипликотивности для f^2	Наличие выделенных элементов в М для операции f^2
Название полукольца	Ассоциативность f^2	Комутативность f^2	e=1	b=^-a^-1
Ассоциативное кольцо	+
Абелево (комутативное) кольцо	+	+
Абелево кольцо с еденицей	+	+	+
Унитарное кольцо (кольцо с еден.)	+		+
Тело	+		+	+
Поле (комутатив.кольцо)	+	+	+	+

Def 16. Группоид - универсальная алгебра с одной бинарной операцией A=‹M,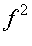›, где 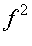:M.

Пример 1: ‹D,+›, ‹D,*›, ‹B(M),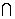›, ‹B(M),\›, ‹B(M),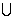›, ‹B(M),›.

Рассматривая алгебраическую бинарную операцию 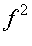как соответствие, её можно задавать рассмотренными выше способами.

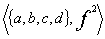Def 17. Нечётким группоидом называется множество всех нечётких подмножеств множества M c одной бинарной алгебраической операцией, т.е. ‹,›.

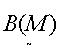Пример2: Для конечного группоида

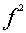
его бинарная операция может быть задана матрицей(таблицей Кели):

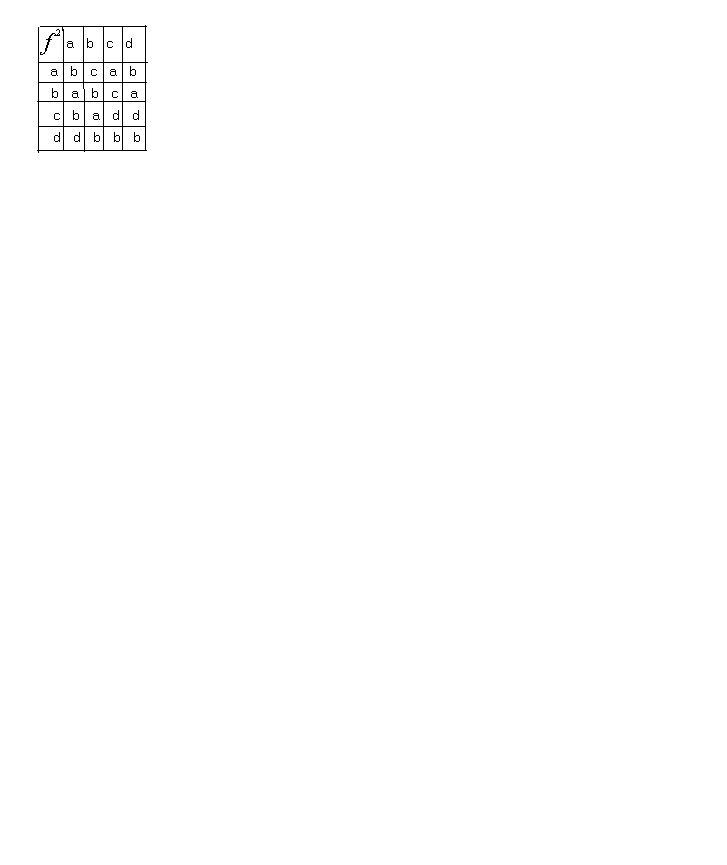
def 18. Нечётким группоидом называется множество всех нечётких подмножеств М с одной заданной бинарной операцией, т.е.

Пример 3: Пусть M={a,b}, а степени элемента принадлежат нечётному множеству {0,,1}. Тогда булево множество имеет вид:

B(M)={{‹a,0›, ‹b,0›,}, {‹a,0›, ‹b, › }, {‹b, ›,‹b,1› }, {‹a, ›, ‹b,0› }, {‹a, ›, ‹b, › }, {‹a, ›, ‹b,1› }, {‹a,1›, ‹b,0› }, {‹a,1›, ‹b, › }, {‹a,1›, ‹b,1› }}

Аналогично: Card 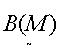=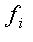, где n=|M|, а m-число степеней принадлежности.

Тогда нечётным группоидом может быть найденный булеан В(м) с алгебраической бинарной операцией, заданной таблицей Кэли:

Здесь каждое нечётное подмножество множества {а,в} сокращенно записано совокупностью степеней принадлежности элементов а и в (так, вместо {‹a,0›, ‹a, 0,5› } и {‹a, 0,5›, ‹b, 0,5› } записано (0, 0,5), (0,5, 1)).

Наделяя бинарную операцию f² группоида определёнными свойствами (идемпотентностью, коммутативностью ассоциативностью), а также задавая структуру множества М относительно этой операции (наличие нейтрального и симметричного элементов) получаем специальные виды группоида – группы, полугруппы и квазигруппы.

Примечание.

1. Группоид, операция которого f² есть операция типа умножения (сложения), называется мультипликативным группоидом (аддитивным группоидом)

2. Если группоид ‹М,f²› мультипликативный, то нейтральный элемент е называется единицей и обозначается 1;

3. Для аддитивного группоида нейтральный элемент называется нулём и обозначается 0.

4. Группоид называется идемпотентным, если его бинарная операция удовлетворяет закону идемпотентности " х Î М (f² ‹х,х› = х).

5. Группоид, операция которого ассоциативна, т.е. " х,у,z Î М (f²‹x, f² ‹y,z› › = f² ‹f² ‹x,y›, z›), называется ассоциативным.

6. Группоид называется коммутативным, или абелевым, если его бинарная операция удовлетворяет закону коммутативности, т.е. если " х,у Î М (f ‹x,y› = f ‹y,x›).

Полугруппы.

Def 19. Ассоциативный группоид есть полугруппа.

Пример. ‹В(m), Ç ›, ‹В(m), È ›, ‹N, +›.

Def 20. Полугруппа с нейтральным элементом (иногда говорят: с сигнатурной единицей, т.е. с нуль-арной операцией отмечающей единицу) называется моноидом.

Иначе: моноид есть кортеж ‹M, f², 1›, для f² и выделенного элемента, для которого справедливы аксиомы:

1. " x,y,z Î M (f² ‹x, f² ‹y,z› › = f² ‹f² ‹x,y›, z›).

2. x´ 1 = 1´ x = x.

Пример. Группоид ‹B(m), È › является моноидом, т.к. операция È - ассоциативна, а единицей служит пустое множество Æ.

Замечание 1. Нечётным моноидом называется любой ассоциативный группоид с единицей.

Примеры. ‹B(u), È; Æ › и ‹B(m), Ç; U› являются нечётными моноидами.

Замечание 2. Коммутативный моноид называют абелевым.

Все приведённые примеры чётных и нечётных моноидов – абелевы.

Группы.

Def 21. Группой называется моноид, в котором для каждого элемента существует и при том единственный обратный элемент q, т.е. ‹М, f²; 1, q›.

Иначе: группой называется пустое множество м с одной бинарной алгебраической операцией f², удовлетворяющее следующим аксиомам:

1. f² ‹a, f² ‹b,c› › = f² ‹f² ‹a,b›, c› для любых а,в, с Î M.

2. f² ‹a,e› = f² ‹e,a› = a для любого а Î M.

3. a´ q = q´ a = e для любых a,q Î M.

Пример. Множество Z с обычной операцией сложения + есть аддитивная группа ‹Z, +, 0, q›. Роль нейтрального элемента е в этом случае играет число 0 (т.е. а+0 = 0+а = а для а Î M), а роль обратного к а элемента – число а (т.е. (-а) + а = а+ (-а) = е = 0).

Пример. Множество всех чётных чисел есть аддитивная группа, являющаяся подгруппой группы ‹Z, +, 0, q›.

Def 22. Группа называется абелевой или коммутативной, если для " а, в Î M бинарная операция f² удовлетворяет аксиоме f² ‹a,b› = f² ‹b,a›

Пример. Множество Q, не содержащее нуля, с операцией обычного умножения является мультипликативной абелевой группой.

В этом случае нейтральным элементом является 1, а обратным к а Î M есть элемент а-1.

Квазигруппы.

Def 23. Квазигруппой (лупой) называется группоид с е и q ‹M, f², e, q›. (т.е. f² не обязательно ассоциативно)

Замечание. В том случае, если в лупе f² ассоциативно, то имеем группу.

Дата добавления: 2014-01-06