Основные понятия. Ошибки в принятой кодовой комбинации можно обнаружить и исправить с помощью помехоустойчивого кода

ПОМЕХОУСТОЙЧИВЫЕ КОДЫ

Ошибки в принятой кодовой комбинации можно обнаружить и исправить с помощью помехоустойчивого кода.

Коды реализуются для режимов обнаружения ошибок, исправления ошибок и одновременного обнаружения и исправления ошибок.

Корректирующие возможности кода определяются его избыточностью, понятие которой состоит в следующем [15,17].

Равномерный (простой) двоичный код имеет множество кодовых комбинаций B={b_i}, мощность которых определяется как N=2ⁿ, где n - разрядность (длина) кода.

Для передачи сообщений из множества B выбирают по определенному закону подмножество AÌB мощностью M кодовых комбинаций, причем M<N. Эти M кодовых комбинаций объявляют разрешенными, а M-N кодовых комбинаций – запрещенными.

Избыточность кода оценивают по формуле

r=1-log₂M/ log₂N.

Множество A разрешенных кодовых комбинаций является помехоустойчивым кодом.

Аналогично можно ошибки записать в виде кодовых комбинаций, причем множество возможных ошибок E={e_i} будет иметь мощность |E|=N, т.е. E=B.

Число ненулевых разрядов в кодовых комбинациях называется весом комбинации. Обозначим кодовую комбинацию через b_i, а вес d_i этой кодовой комбинации – через w(d_i). Если b_i=0101101, то w(d_i)=4.

Кратность ошибки равна весу комбинации ошибок e_i.

Пусть передается кодовая комбинация a_iÎA, а принимается кодовая комбинация b_iÎB, причем b_i может принадлежать и не принадлежать множеству A. Кодовая комбинация b_i есть результат воздействия ошибки на кодовую комбинацию a_i, т.е. b_i=a_iÅ e_i. Безошибочной будет передача в том случае, если b_i=a_i, т.е. w(e_i)=0. При w(e_i)¹0®b_i¹a_i и возможно, что b_iÎA - необнаруженная ошибка или b_iÏA - обнаруженная ошибка в принятой кодовой комбинации.

Идея обнаружения ошибок состоит в следующем.

Принятая кодовая комбинация декодируется автоматическим устройством – декодером. В результате декодирования принимается решение, содержит или нет кодовая комбинация ошибки. При этом проверяются условия: а) b_iÎA и b_iÏВ/A; б) b_iÎВ/A и b_iÏA. При выполнении условия б) считается, что кодовая комбинация содержит ошибку.

Очевидно, что возможно обнаружить те ошибки, которые переводят кодовую комбинацию a_i в множество В/A, причем число этих комбинаций ошибок равно N-M. Остальные M комбинации ошибок не обнаруживаются, т.к. они переводят одну разрешенную кодовую комбинацию в другую кодовую комбинацию.

Пример. Пусть n=4. Множество простого кода В ={0000, 0001, 0010, 0011, 0100, …, 1111}. Выберем множество A по закону 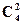. Тогда множество A ={0011, 0101, 0110, 1001, 1010, 1100}, а множество В/A содержит оставшиеся комбинации из множества простого кода. Множество E = В. Пусть e =0110, a =1000, тогда при поразрядном суммировании e и a по модулю два получим b=aÅe= 1110. Так как кодовая комбинация b_iÎВ/A, то ошибка обнаружена.

Идея исправления ошибок состоит в следующем. Множество простого кода В разбивается на M=2^m подмножеств В_i, причем |В_i|=2^n-m. В каждое множество В_i входит одна разрешенная кодовая комбинация a_iÎВ_i и (2^n-m-1) запрещенных кодовых комбинаций.

При декодировании принятой кодовой комбинаций b_i проверяется, какому из подмножеств В_j (j=1,1,…, 2^n-m) принадлежит комбинация b_i. Если b_iÎВ_j, то принимается решение, что передавалась кодовая комбинация a_j. Исправляются все ошибки, в результате которых b_iÎВ_j, причем их количество 2^n-m-1. Все остальные ошибки, которые “выводят” b_i из множества В_j (b_iÏВ_j), не исправляются.

Пример. Множество простого кода В ={0000, 0001, 0010, 0011, 0100, …, 1111}. M=2¹, |В_i|=2^3-1=2²=4. Построим множества В₁ ={101, 001, 111, 100} и В₂ ={010, 110, 011, 000}. Разрешенные кодовые комбинации 101 и 010.

Если a_i =101 и e =111, то b_j=a_iÅe =010. Следовательно, ошибка не обнаружена.

Если a_i =101 и e =001, то b_j=a_iÅe =100, ошибка обнаружена.

При построении кода решаются две задачи:

1) как выбрать множество А (задача кодирования);

2) как разбить множество В на подмножества В_i (задача декодирования).

Дата добавления: 2014-01-06