Построение циклических кодов

Сведения из алгебры полиномов

ЦИКЛИЧЕСКИЕ КОДЫ

Описание циклических кодов основано на представлении комбинаций в виде многочленов (полиномов) от одной фиктивной переменной х с коэффициентами [17]. При наименьшем разряде полинома присутствует степень x⁰, а при наибольшем – степень x^n-1, где n - длина разрядов. Например, комбинация 11011011 в виде полинома будет иметь вид х⁷+х⁶+х⁴+х³+х+1. Заметим, что арифметический знак + здесь рассматривается как фиктивная операция.

Сложение двух полиномов выполняется как поразрядное суммирование по модулю два (mod2). Например, b₁=1011=х³+х+1, а b₂=11101=х⁴+х³+х²+1. Тогда b₁Åb₁ = х³+х+1+х⁴+х³+х²+1=х⁴+х²+х.

Умножение двух полиномов осуществляется в идеале поля Галуа (хⁿ+1). Происходит это следующим образом. Пусть n=4, b₁=0011=х+1, а b₂=0110=х²+х. Тогда b₁b₂ =(х+1)(х²+х)=х³+х. Пусть n=4, b₁(х)=х³+х², а b₂(х)=х³+х+1. Тогда в обычной алгебре b₁b₂ = х⁶+х⁵+х⁴+х², а по модулю (х⁴+1) b₁b₂ = Rem[(х⁶+х⁵+х⁴+х²)/(х⁴+1)]=х+1, где Rem[.] - остатокот деления. Следовательно, b₁b₂ = х+1 (0011).

Таблица 5.1

Синдром ошибки	Принимаемое решение
	Нет ошибок. Информация выдается получателю
	Ошибка в первом контрольном разряде. Информация выдается получателю
	Ошибка во втором контрольном разряде. Информация выдается получателю
	Ошибка в третьем контрольном разряде. Информация выдается получателю
	Ошибка в четвертом контрольном разряде. Информация выдается получателю
	Ошибка в первом разряде. Информация после исправления выдается получателю
	Ошибка во втором разряде. Информация после исправления выдается получателю
	Ошибка в третьем разряде. Информация после исправления выдается получателю
	Ошибка в четвертом разряде. Информация после исправления выдается получателю
	Ошибка в пятом разряде. Информация после исправления выдается получателю
Остальные коды синдрома	Ошибка не обнаружена. Информация стирается

Циклические коды являются частным случаем групповых кодов и однозначно задаются с помощью порождающего (образующего) полинома

g(x)=g_kx^k+g_k-1x^k-1+…+g₁x+g₀.

Особенности порождающего полинома:

- порождающий полином g(x) имеет наименьшую степень среди многочленов данного идеала (хⁿ+1);

- свободный член g⁰ всегда не равен нулю;

- любой многочлен циклической группы делится на g(x) без остатка;

- g(x) является делителем для двучлена (хⁿ+1).

Так как любое кодовое слово b(х) должно делиться на g(x), то

b(х)=n(х)g(х). (4.1)

Соотношение (4.1) описывает процесс кодирования слова. n=(n_m-1,n_m-2,…,n₀) - вектор первичного (безызбыточного) кода длиной m разрядов, записанный в виде полинома

.

В результате применения соотношения (4.1) можно построить неразделимый циклический код, для которого образующая матрица имеет следующий вид:

.

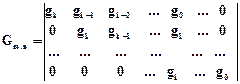Желательно циклический код представлять в виде разделимого кода, т.е. в кодовой комбинации b(х)=b_n-1x^n-1+b_n-2x^n-2+…+b₁x+b₀, коэффициенты кодового полинома при x^n-1, x^n-2,…,x^k - информационные символы, а при x^k-1,x^k-2, …,x,1 - контрольные символы.

Для получения разделимого циклического кода достаточно вычислить остатки от деления произведения x^kn_i(х), (i-0,1,…m-1) на порождающий полином g(x).

Если выбрать в качестве базисных кодовых полиномов xⁱx^k+R_i(х), то получим для разделимого кода порождающую матрицу в канонической форме G_m,n=|I_mR_m,k|. Причем,

. (4.2)

Пример. Полином g(х)=х³+х²+1 порождает циклический код (7,4). Информационные элементы кодовых комбинаций, используемые в качестве строк образующей матрицы, имеют следующую запись: n_i(х)=х⁰, n_i(х)=х¹, n_i(х)=х², n_i(х)=х³.

Тогда, R₀(х)=Rem[x^kx⁰/g(x)]=Rem[x³/(х³+х²+1)]=х²+1, R₁(х)=Rem[x⁴/(х³+х²+1)]=х²+x+1, R₂(х)=Rem[x⁵/(х³+х²+1)]=x+1, R₆(х)=Rem[x⁶/(х³+х²+1)]=x²+x.

Образующая матрица будет иметь вид

.

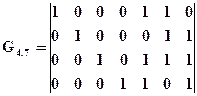Дата добавления: 2014-01-06