
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы обнаружения и исправления ошибок
|
|
|
|
Пусть под влиянием помехи e(x) в канале связи передаваемая кодовая комбинация b(х) переходит в принимаемую кодовую комбинацию b*(х), т.е. b*(х)=b(х)Åe(x)..
Помимо порождающего полинома существует проверочный полином h(x), причем
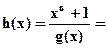 h(x)=hmxm+hm-1xm-1+…+h1x+h0.
h(x)=hmxm+hm-1xm-1+…+h1x+h0.
Проверочная матрица циклического кода имеет следующий вид
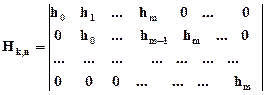 .
.
Пример. Для циклического кода (7,4) g(х)=х3+х2+1, k=3. Тогда проверочный полином h(x)=(x7+1)/(х3+х2+1)=x4+x3+x2+1. Проверочная матрица имеет следующий вид
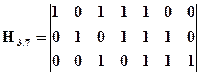 .
.
Если умножить b*(х) на полином h(x), то получим
b*(х)h(x)=b(х)h(x)Åe(x)h(x)=e(x)h(x) по mod(xn+1),
т.к. b(х)h(x)=b(х)(xn+1)/g(х)=0.
При коррекции ошибок с использованием свойств проверочного полинома последовательность
d(x)=e(x)h(x) по mod(xn+1)
есть опознователь (синдром) ошибки.
Если e(x)h(x)¹0 по mod(xn+1), то принятая кодовая комбинация b*(х) не совпадает ни с одним из элементов идеала (не принадлежит циклическому коду), что свидетельствует о наличии ошибки в принятой кодовой комбинации.
Многочлены ошибок различимы, если ei(x)h(x)¹ej(x)h(x).
Допустим, полиномы ei(x) и ej(x) различимы, причем ej(x)=xrei(x), r=1,2,…,n-1. Тогда dj(x)=ej(x)h(x)=xrei(x)h(x)=xrdi(x) по mod(xn+1), т.е. dj(x) есть результат циклического сдвига на r шагов влево полинома di(x). Это упрощает процедуру коррекции ошибок.
Пример. Циклический код (7,4) имеет проверочный полином h(x)=x4+x3+x2+1, d=3, s=1.
Для исправления одиночных ошибок решающая схема декодирующего устройства настроена на корректор d6(x), соответствующий ошибке старшего разряда, что соответствует ошибке e6(x)=x6. Определим корректор ошибки старшего разряда
d6(x)=e6(x)h(x)=x6(x4+x3+x2+1)=x6+x3+x2+х по mod (x7+1), d6=1001110.
d(x)=b*(х)h(x)=(x5+x2) (x4+x3+x2+1)=x6+x4+x+1 (1010011) по mod (x7+1), d(x)¹d6(x).
Следовательно, принятая кодовая комбинация не содержит ошибки в старшем (шестом разряде). Найденный корректор d(x) сдвигаем на один разряд влево, получим d’=0100111, d’(x)¹d6(x), следовательно, и в пятом разряде принятой кодовой комбинации нет ошибки. Затем уже корректор d”(x) сдвигаем на один разряд влево, получим d’’=1001110, d’’(x)=d6(x), следовательно, в четвертом разряде принятой кодовой комбинации есть ошибка.
С другой стороны, т.к. h(x)=(xn+1)/g(x), то синдром ошибки принятой кодовой комбинации определится
 .
.
Аналогично, если ej(x)=xrei(x), то
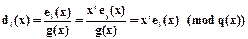 ,
,
т.е. dj(x) образуется в результате сдвига di(x) на r шагов влево.
Пример. Циклический код (7,4) имеет порождающий полином g(x)=x3+x2+1, d=3, s=1. Корректор настроен на ошибку старшего разряда e6(x)=x6. Корректор ошибки старшего разряда
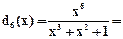 x2+x по mod g(x).
x2+x по mod g(x).
Пусть b=0110100, e(x)=x4, т.е. b*=0100100. Корректор ошибки в принятой кодовой комбинации b* равен
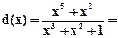 x2+x+1 по mod g(x).
x2+x+1 по mod g(x).
Найденный корректор d(x) не равен d6(x), следовательно, принятая кодовая комбинация не содержит ошибки в старшем разряде. Сдвигаем d(x) на один разряд влево, получим d’(x)=d(x)х=x3+x2+х=х+1 по mod (х3+x2+1),. Так как d’(x)¹d6(x),, то в пятом разряде b* также нет ошибки. Выполняем еще один сдвиг d(x) влево, получим d’’(x)=d’(x)x=x2+х. d’’(x)=d6(x), следовательно, в четвертом разряде принятой кодовой комбинации есть ошибка.
Условия выбора порождающего полинома следующие.
Задано m информационных символов, известны значения r и s. Определяем значения d и k.
Число k соответствует степени порождающего полинома g(x), степень полинома должна быть не менее числа k.
Полином g(x) является делителем двучлена (xn+1).
Корректирующая способность кода будет тем выше, чем больше остатков от деления можно получить от деления xn на полином g(x) (представляется как единица со многими нулями). Остатки от деления отличаются друг от друга в d-2 и более разрядах, вес остатков более либо равен d-1.
Полином g(x) может быть произведением двух и более простых полиномов, входящих в разложение (xn+1).
Число ненулевых коэффициентов в полиноме g(x) должно быть больше либо равно d.
В табл.4.1 приведены разложения полинома (xn+1) на неприводимые сомножители.
В табл. 5.2 сомножитель (x+1), входящий в разложение полинома (xn+1) любой степени, не приведен, но его следует учитывать при выборе порождающего полинома.
С целью сокращения записи многочлены разложения (xn+1) кодированы восьмеричным кодом: 0«000, 1«001, 2«010, 3«011, 4«100, 5«101, 6«110, 7«111.
Коэффициенты многочленов в двоичной записи расположены в порядке убывания, так что коэффициент при слагаемом высшего порядка расположен слева.
Например, если степень полинома n =15, то из соответствующей строки выписываем кодированные значения 23, 37, 7, 31. Перепишем в восьмеричном коде (010011)(011111)(111)(011001). Разложение полинома 15-й степени с учетом (x+1) примет вид (x15+1)=(x+1)(x4+x+1)(x4+x3+x2+x+1)(x2+x+1)(x4+x3+1).
Таблица 5.2
| Степень полинома | Неприводимые сомножители | Старшая степень сомножителя |
| 13, 17 | 3, 3 | |
| 111, 7 | 6, 2 | |
| 3, 37 | 1, 4 | |
| 3, 13, 13, 15, 15 | 1, 3, 3, 3, 3 | |
| 23, 37, 7, 31 | 4, 4, 2, 4 | |
| 727, 471 | 8, 8 | |
| 127, 15, 165, 7, 13 | 6, 3, 6, 2, 3 | |
| 5343, 6165 | 11, 11 | |
| 4102041, 37 | 20, 4 | |
| 1001001, 111, 7 | 18, 6, 2 | |
| 45, 75, 67, 57, 73, 51 | 5, 5, 5, 5, 5, 5 | |
| 3043, 3777, 2251, 7 | 10, 10, 10, 2 | |
| 16475, 13627, 13, 37, 15 | 12, 12, 3, 4, 3 | |
| 13617, 17777, 17075, 7 | 12, 12, 12, 2 | |
| 6647133, 5747175 | 20, 20 | |
| 52225, 47771, 64213 | 14, 14, 14 | |
| 10011, 23, 111, 11001, 37, 7, 31 | 12, 4, 6, 12, 4, 2, 4 | |
| 43073357, 75667061 | 23, 23 | |
| 10040001, 10000201, 13, 15 | 21, 21, 3, 3 | |
| 763, 727, 433, 471 | 8, 8, 8, 8 |
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 540; Нарушение авторских прав?; Мы поможем в написании вашей работы!