Размещения с повторениями и без повторений

Используя цифры 7, 4 и 5, можно образовать различные двузнач­ные числа: 77, 74, 75, 47, 44, 45, 57, 54, 55. В записи этих чисел цифры повторяются.

С теоретико-множественной точки зрения запись любого двузнач­ного числа – это кортеж длины 2. Записывая различные двузначные числа с помощью цифр 7, 4 и 5, мы по сути дела образовывали из дан­ных трех цифр различные кортежи длины 2 с повторяющимися эле­ментами. В комбинаторике такие кортежи называют размещениями с повторениями из трех элементов по два элемента.

Определение. Размещение с повторениями из k элементов по т элементов - это кортеж, составленный из т элементов k-элементного множества.

Из определения следует, что два размещения из k элементов по т элементов отличаются друг от друга либо составом элементов, либо порядком их расположения.

Например, два двузначных числа из перечисленных выше (а это размещения из трех элементов по два) отличаются друг от друга либо составом элементов (74 и 75), либо порядком их расположения (74 и 47).

Число всевозможных размещений с повторениями из k элементов по т элементов обозначают и подсчитывают по формуле = k^m.

Выведем эту формулу.

Пусть в множестве X содержится k элементов. Будем образовывать из них различные кортежи по т элементов. Такие кортежи образуют множество

X´ X´... ´ X, содержащее т множителей. По правилу произведения

п (X´ X´... ´ X)= 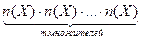= = 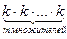k^m.

Следовательно, = k^m.

Пользуясь этой формулой, легко подсчитать, сколько двузначных чисел можно записать, используя цифры 7, 4 и 5. Так как речь идет о размещениях с повторениями из трех элементов по два, то = 3² = 9.

Нередко встречаются задачи, в которых требуется подсчитать чис­ло кортежей длины т, образованных из k элементов некоторого мно­жества, но при условии, что элементы в кортеже не повторяются. Та­кие кортежи называются размещениями без повторений из k элемен­тов по т элементов.

Определение. Размещение без повторений из k элементов по т элементов - это кортеж, составленный из т неповторяющихся элементов множества, в котором k элементов.

Число всевозможных размещений без повторений из k элементов по т элементов обозначают и подсчитывают по формуле

=k^. (k–1)^. …^. (k–m+1).

Задание! Вывести эту формулу самостоятельно.

Например, число двузначных чисел, записанных с помощью цифр 7, 4 и 5 так, что цифры в записи числа не повторяются, есть число размещений без повторений из трех элементов по два: 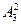= 3 ^.(3 –1) = 3 ^. 2 = 6.

Дата добавления: 2014-01-06