Перестановки без повторений и с повторениями

Задача. Сколько всевозможных трехзначных чисел можно запи­сать, используя цифры 7, 4 и 5, так, чтобы цифры в записи числа не повторялись.

Решение. В задаче рассматриваются размещения без повторений из трех элементов по три, и их число можно подсчитать по формуле:

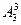= 3 ^.(3 –1)^.(3–2) = 3 ^. 2^. 1 = 6.

Эти числа таковы: 745, 754, 475, 457, 547, 574.

Заметим, что в данном случае разные числа получаются в резуль­тате перестановки цифр. Поэтому размещения из k элементов по k эле­ментов называют перестановками из k элементов без повторений.

Число перестановок без повторений из k элементов обознача­ют P_k и подсчитывают по формуле P_k = k!, где k! = 1^. 2^. 3^.... ^.k и читают «k факториал». Считают, что 1! = 1, 0!= 1. Например, 5! = 120; 7! = 5040.

Таким образом, перестановки без повторений – это частный случай размещения без повторений.

Определение. Кортежи длины m, в которые входит элемент а₁ – m₁ раз, элемент а₂ – m₂ раз, …, элемент а_k – m_k раз (m₁+m₂+…+m_k=m), называют перестановками с повторениями состава (m_1,m_2,…,m_k).

Их число выражается формулой: Р(m_1,m_2,…,m_k) =.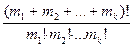

Задача. Сколькими способами можно расставить на первой линии шахматной доски 6 белых пешек и 2 черных?

Решение. Р(6,2)=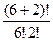=28.

Дата добавления: 2014-01-06