
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правило Лопиталя. Формула Тейлора
|
|
|
|
В случае неопределенностей вида 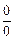 и
и 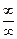 при вычислении пределов часто бывает полезным правило Лопиталя, которое задается следующей теоремой.
при вычислении пределов часто бывает полезным правило Лопиталя, которое задается следующей теоремой.
Теорема 1. Пусть функции f (x) и g (x) удовлетворяют следующим условиям:
1) определены и дифференцируемы на интервале (a; b), за исключением, быть может, точки 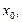 причем
причем 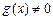 и
и 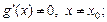
2) 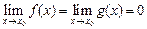 (либо
(либо 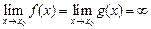 );
);
3) существует предел 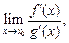 тогда существует предел отношений функций
тогда существует предел отношений функций 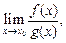 причем
причем
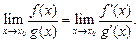 (17.19)
(17.19)
Правило Лопиталя можно использовать последовательно несколько раз.
Аналогичное правило верно в случае 
Если при вычислении пределов возникает неопределенность иного вида, то вначале пределы необходимо свести к неопределенности вида  или
или 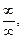 а затем использовать правило Лопиталя.
а затем использовать правило Лопиталя.
В частности, выражения, которые приводят к неопределенностям вида 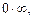
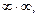 тождественно преобразуют к такому выражению, которое приводят к неопределенности вида
тождественно преобразуют к такому выражению, которое приводят к неопределенности вида 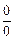 или
или 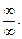
Неопределенности вида 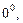
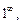
 возникают при рассмотрении функции типа
возникают при рассмотрении функции типа 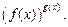 С помощью тождества
С помощью тождества
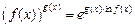 (17.20)
(17.20)
они сводятся к неопределенности вида 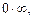 а затем – к
а затем – к 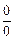 или
или 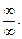
Если функция f (x) имеет в некоторой окрестности точки 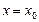 производные до (
производные до (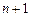 )-го порядка включительно, то при
)-го порядка включительно, то при 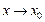 верна формула Тейлора:
верна формула Тейлора:
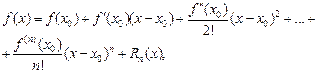 (17.21)
(17.21)
где 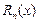 – остаточный член формулы Тейлора.
– остаточный член формулы Тейлора.
Существует несколько форм записи остаточного члена. В частности, в форме Лагранжа:
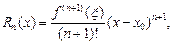
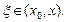
Если в формуле Тейлора 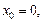 получим частный вид формулы Тейлора – формулу Маклорена:
получим частный вид формулы Тейлора – формулу Маклорена:
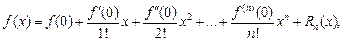
где 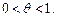
Верны следующие формулы Маклорена:
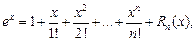 (17.22)
(17.22)
где 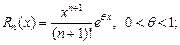
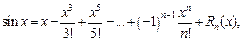
где 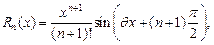
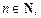
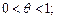
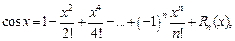 (17.23)
(17.23)
где 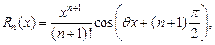
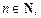
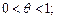
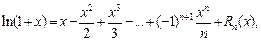 (17.24)
(17.24)
где 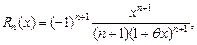
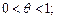
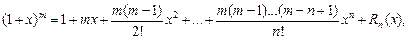
где 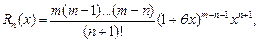
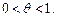
Формулы Маклорена могут быть использованы в приближенных вычислениях. При этом абсолютная погрешность приближения в случае чередования знаков в формуле Маклорена не превосходит абсолютной величины первого отбрасываемого слагаемого.
Задания
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 664; Нарушение авторских прав?; Мы поможем в написании вашей работы!