
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И наименьшее значение функций на промежутке
|
|
|
|
Исследование функций. Наибольшее
III уровень
3.1. Вычислите предел функции с помощью правила Лопиталя:
1)  2)
2) 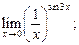
3) 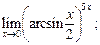 4)
4) 
5)  6)
6) 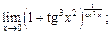
7) 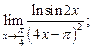 8)
8) 
3.2. Вычислите предел функции различными способами:
1)  2)
2) 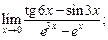
3)  4)
4) 
5)  6)
6) 
7) 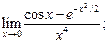 8)
8) 
3.3. Используя известные формулы Маклорена, разложите функцию f (x) по степеням x (запишите первые 5 слагаемых):
1) 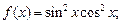 2)
2) 
3)  4)
4) 
Всюду далее функция f (x) определена на рассматриваемых промежутках.
Теорема 1 (достаточное условие монотонности). Дифференцируемая на (a, b) функция возрастает (убывает) на этом интервале тогда и только тогда, когда 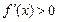
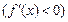

Точка х 0 называется точкой локального максимума (минимума) функции f (x), если существует некоторая окрестность точки 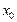 такая, что для всех x из этой окрестности выполняется неравенство
такая, что для всех x из этой окрестности выполняется неравенство 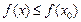

Значение 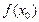 называется локальным максимумом (минимумом) функции.
называется локальным максимумом (минимумом) функции.
Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются экстремумом функции.
Теорема 2 (необходимое условие существования экстремума функции). Если в точке 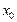 функция f (x) достигает экстремума, то ее производная в этой точке равна нулю или не существует.
функция f (x) достигает экстремума, то ее производная в этой точке равна нулю или не существует.
Те точки из области определения функции f (x), в которых производная функции f (x) обращается в нуль или не существует, называют критическими. Исследование функции на экстремум начинается с нахождения критических точек. Однако не в каждой критической точке существует экстремум. Для того чтобы определить точки экстремума, используют достаточные условия (признаки экстремума).
Теорема 3 (первый признак экстремума функции). Пусть 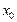 – критическая точка непрерывной функции f (x). Если в некоторой окрестности точки
– критическая точка непрерывной функции f (x). Если в некоторой окрестности точки 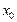 выполняется условие
выполняется условие
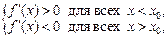
то 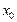 – точка локального максимума;
– точка локального максимума;
если выполняется условие

то 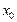 – точка локального минимума.
– точка локального минимума.
Если производная 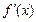 имеет один и тот же знак в левой и правой полуокрестности точки
имеет один и тот же знак в левой и правой полуокрестности точки 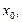 то
то 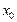 не является точкой экстремума.
не является точкой экстремума.
Теорема 4 (второй признак экстремума функции). Пусть 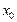 – критическая точка дважды дифференцируемой функции f (x). Тогда
– критическая точка дважды дифференцируемой функции f (x). Тогда 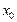 является точкой локального минимума функции f (x), если
является точкой локального минимума функции f (x), если  и точкой локального максимума, если
и точкой локального максимума, если 
Теорема 5 (третий признак экстремума функции). Пусть f (x) – n раз непрерывно дифференцируемая в критической точке 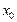 функция и
функция и 
 Тогда:
Тогда:
1) если n – четное и 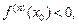 то
то 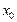 – точка локального максимума;
– точка локального максимума;
2) если n – четное и 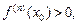 то
то 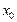 – точка локального минимума;
– точка локального минимума;
3) если n – нечетное, то 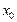 не является точкой локального экстремума.
не является точкой локального экстремума.
З а м е ч а н и е 1. При исследовании функции и построении ее графика целесообразно использовать первый признак экстремума, так как одновременно получаем возможность исследования функции на монотонность.
Точка 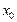 называется точкой глобального максимума (минимума) функции f (x) на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство
называется точкой глобального максимума (минимума) функции f (x) на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство 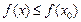

Точки глобального максимума и минимума называются точками глобального экстремума. Значения функции в этих точках называются соответственно глобальным максимумом (наибольшим значением) и глобальным минимумом (наименьшим значением).
Теорема 6 (Вейерштрасса). Если функция f (x) непрерывна на отрезке, то она достигает на нем своих наименьшего и наибольшего значений.
Непрерывная на отрезке функция достигает наименьшего (наибольшего) значений либо на концах отрезка, либо в точках ее локального экстремума.
Для отыскания глобального экстремума функции f (x) на отрезке [ a, b ] необходимо:
1) найти производную 
2) найти критические точки функции;
3) найти значения функции на концах отрезка, т. е. f (a) и f (b), а также в критических точках, принадлежащих (a, b);
4) из всех полученных значений функции определить наибольшее и наименьшее ее значения.
График функции 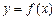 называется вогнутым (выпуклым вниз) на (a, b), если дуга кривой
называется вогнутым (выпуклым вниз) на (a, b), если дуга кривой 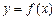 на этом интервале расположена выше любой касательной, проведенной к графику этой функции (рис. 17.1).
на этом интервале расположена выше любой касательной, проведенной к графику этой функции (рис. 17.1).
 |
Рис. 17.1
График функции 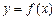 называется выпуклым (выпуклым вверх) на (a, b), если дуга кривой
называется выпуклым (выпуклым вверх) на (a, b), если дуга кривой 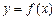 на этом интервале расположена ниже любой касательной, проведенной к графику этой функции (рис. 17.2).
на этом интервале расположена ниже любой касательной, проведенной к графику этой функции (рис. 17.2).
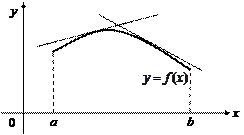 |
Рис. 17.2
Теорема 7. Если функция f (x) дважды дифференцируема на (a, b) и 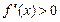
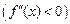 всюду на этом интервале, то график функции вогнутый (выпуклый) на (a, b).
всюду на этом интервале, то график функции вогнутый (выпуклый) на (a, b).
Точка 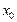 такая, что график функции
такая, что график функции 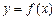 меняет выпуклость на вогнутость или наоборот, проходя через
меняет выпуклость на вогнутость или наоборот, проходя через  , называется точкой перегиба (рис. 17.3).
, называется точкой перегиба (рис. 17.3).
 |
Рис. 17.3
Для нахождения точек перегиба вначале находят критические точки 2-го рода – те значения x, для которых 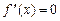 или
или 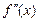 не существует. Далее используют достаточные условия перегиба.
не существует. Далее используют достаточные условия перегиба.
Теорема 8 (первый признак перегиба). Если функция f (x) непрерывна в критической точке 2-го рода 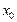 и ее вторая производная
и ее вторая производная 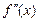 имеет различные знаки слева и справа от
имеет различные знаки слева и справа от 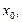 то
то 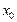 – точка перегиба.
– точка перегиба.
Теорема 9 (второй признак перегиба). Если функция f (x) имеет непрерывную производную  в точке
в точке 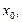 в которой
в которой  то
то 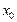 – точка перегиба.
– точка перегиба.
З а м е ч а н и е 2. При исследовании функции и построении ее графика целесообразно использовать первый признак перегиба, так как одновременно получаем возможность исследования графика функции на выпуклость и вогнутость.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 626; Нарушение авторских прав?; Мы поможем в написании вашей работы!