Проецирование точки

3.1 Проецирование точки на две и три плоскости проекций

Если поместить точку А, находящуюся в пространстве, относи­тельно двух плоскостей проекций П₁, и П₂, опустив из нее перпенди­куляры на эти плоскости, получают точки А₁, и А₂, которые являются ортогональными проекциями точки А относительно плоскостей про­екций П₁, и П₂. Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы. Так, для точки А:

[AA₁]=[A₂A_x] = z_A;

[AA₂]=[A₁A_х,] = y_A.

Плоскость прямоугольника А₁АА₂А_x, перпендикулярна к оси x, а линии пересечений плоскостей П₁П₂ и плоскости А₁АА₂А_x являются прямыми А₁А_х и А₂А_x перпендикулярными к оси х в точке А_x. Изображение точки и её проекций является пространственным чертежом, это наглядно, но не всегда удобно для практики.

Чтобы получить плоский чертёж, поворачивают плоскость П₁, во­круг оси х и совмещают её с плоскостью П₂ (рисунок 3.1).

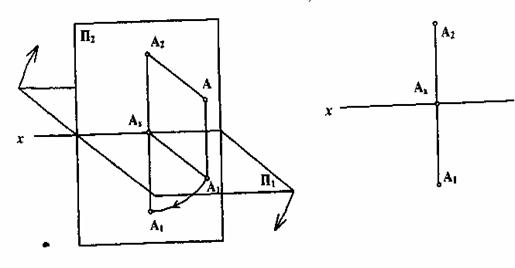
Рисунок 3.1 Рисунок 3.2

Проекции а₁ и А₂ оказываются на одной линии, которая называ­ется линией проекционной связи. Она перпендикулярна к оси х (рисунок 3.2).

При проецировании точки А на три плоскости проекций от плос­кости П₃ она отстоит на расстоянии АА₃ (рисунок 3.3). При этом, анало­гично вышесказанному:

[A₂A_Z] = [АА₃] = [0А_х] = x_А;

[A₃A_Z] = [AA₂] = [0A_Y] = y_A;

[A₃A_Y] =[AA₁] = 0A_Z] = z _a.

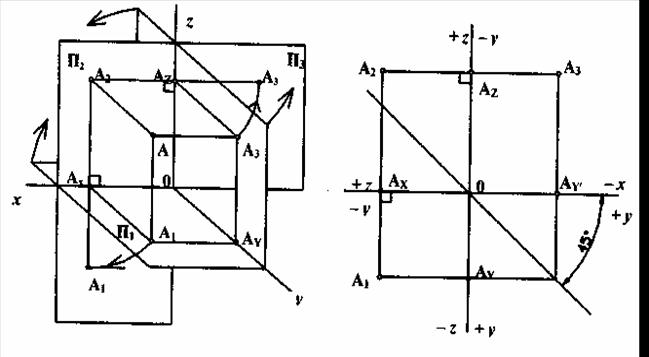
Рисунок 3.3 Рисунок 3.4

Для получения плоского чертежа в этом случае уже две плоскости П₁ и П₃ совмещаются с плоскостью П₂ путём поворота их соответст­венно вокруг осей х и у. При этом ось у, как бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показа­но на рисунке 3.4. Профильная проекция А₃ точки А находится на пересе­чении линий связи A₂A_ZA₃ и A₁A_YA₃ (расстояние 0А_у = 0Ау). Перенос точки A_Y в точку A_Y понятен из чертежа, а сам отрезок есть ничто иное, как координата y_a.

На плоском трёхмерном чертеже (трехпроекционный комплексный чертеж) положительное направление оси х совпадает с отрицательным направлением оси у, а отрицательное направление оси х с положительным направлением оси у.

Это не означает, что модули этих величин обязательно равны ме­жду собой, т.е. [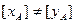] (в частном случае это равенство может быть). Те же рассуждения будут справедливы и в отношении направ­лений осей z и y (рисунок 3.4).

Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, пер­пендикулярной к оси x, а фронтальная и профильная проекции точки А лежат на одной проекционной линии связи, перпендикулярной к оси z.

3.2 Определение по плоскому чертежу принадлежности точки
тому или другому октанту пространства

Точка, например А, принадлежит

· I или V октанту, если её проекция А₁(лежит под осью х, а
А₂ - над осью х;

· II или VI октанту, если и a₁ и А₂ лежат над осью х;

· III или VII октанту, если A₁ лежит над осью х, а А₂ - под ней;

· IV или VIII октанту, если и a₁ и А₂ лежат под осью х.

3.3 Определение по плоскому чертежу принадлежности точки
плоскостям проекций

Например, точка А принадлежит:

-горизонтальной плоскости проекций П₁ если 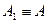, а А₂оси х и A₃ y;

-фронтальной плоскости проекций П₂, если 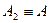, а А₁оси х и A₃ z;

-профильной плоскости проекций П₃, если , а А₁оси y и A₂ оси z;

Любая точка лежит на оси проекций, если её смежные две проек­ции совпадают. Так, точка А лежит на оси х, если a₁ совпадает с А₂; на оси у, если A₂ совпадает с А₃, и оси z, если А₂ совпадает с А₃.

3.4 Правила знаков координат проекции точки

Координата х любой точки есть не что иное, как расстояние от этой точки до профильной плоскости проекций. Учитывая, что рас­стояние измеряется перпендикулярно к плоскости, на чертеже прово­дится ось х. Координата х положительна для точек, находящихся cлева от профильной плоскости проекций П₃, и отрицательна для нахо­дящихся от неё справа. Координата x всегда откладывается от начала координат (точка 0).

Положительное значение координаты у будет для точек, находя­щихся перед фронтальной плоскостью проекций П₂отрицательное - для расположенных за ней. Координату у можно откладывать непо­средственно от оси х (вниз - положительное значение, вверх - отри­цательное).

Положительное значение координаты z будет для точек, располо­женных выше горизонтальной плоскости проекций П₁ а отрицатель­ное - если точки находятся ниже П₁. Координату z на чертеже также можно откладывать от оси x (вверх - положительное значение, вниз - отрицательное).

Если рассматривать все восемь октантов пространства, то знаки для всех трёх координат точки (х, у, z) приведены в таблице 3.1 и на­глядно представлены на рисунках 3.3 и 3.4.

Таблица 3.1

Координаты	Октанты
	I	II	III	IV	V	VI	VII	VIII
x	+	+	+	+	—	—	—	—
y	+	—	—	+	+	—	—	+
z	+	+	—	—	+	+	—	—

Дата добавления: 2014-01-06