Плоскость. Плоскость задается тремя произвольными точками, не принадле­жащими одной прямой

5.1 Задание плоскости

Плоскость задается тремя произвольными точками, не принадле­жащими одной прямой. Плоскость в пространстве можно задать:

· тремя точками, не лежащими на одной прямой (рисунок 5.1, а);

· прямой и не принадлежащей ей точкой (рисунок 5.1, б);

· двумя пересекающимися прямыми (рисунок 5.1, в);

· двумя параллельными прямыми (рисунок 5.1, г);

· любой плоской фигурой (рисунок 5.1, д).

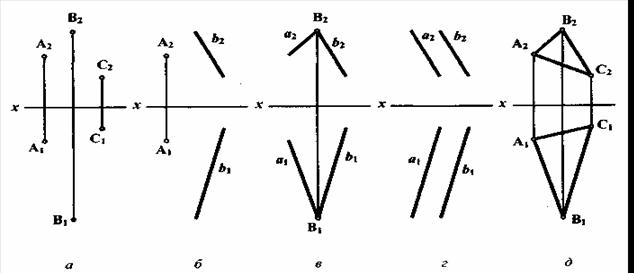
Рисунок 5.1

Каждый из перечисленных способов задания плоскости допускает переход к любому другому, т.к. положение прямой в плоскости опре­деляется двумя ее точками или одной точкой и направлением этой прямой.

Часто применяется способ задания плоскости с помощью прямых линий (взаимно пересекающихся или параллельных), по которым данная плоскость пересекается с плоскостями проекций П₁П₂, П₃. Кроме этого - это задание плоскости следами, при этом сохраняется наглядность изображения (рисунок 5.2).

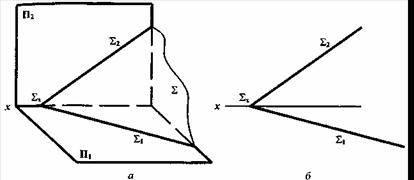
Рисунок 5.2

5.2 Следы плоскости.

Линия пересечения рассматриваемой плоскости с плоскостью проекций (П₁, П₂, П₃ ) называется следом плоскости. Иными словами, след плоскости - это прямая, лежащая в плоскости проекций. Следу присваивается наименование той плоскости проекций, которой он принадлежит. Например, горизонтальный след получен при пересече­нии заданной плоскости с плоскостью П₁ и обозначается 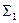, фрон­тальный — с плоскостью П₂ ( 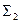), профильный — с плоскостью П₃(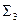). Два следа одной и той же плоскости пересекаются на оси про­екции в точке, называемой точкой схода следов. Каждый из следов плоскости совпадает со своей одноименной проекцией, остальные проекции оказываются лежащими на осях. Например, горизонтальный след плоскости Σ(рисунок 5.2) совпадает со своей горизонтальной проек­цией 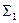, фронтальная его проекция находится на оси х, а профильная на оси у. По расположению следов плоскости можно судить о по­ложении данной плоскости в пространстве относительно плоскостей проекций П₁,П₂, П₃.

5.3 Положение плоскости относительно плоскостей проекций

Любая, произвольно взятая в пространстве плоскость, может за­нимать общее или частное положение. Плоскостью общего положения называется плоскость, которая не перпендикулярна ни к одной из плоскостей проекций (см. рисунок 5.2). Все остальные плоскости (кроме плоскостей проекций) относятся к плоскостям частного положения и подразделяются на проецирующие плоскости и плоскости уровня. |Проецирующей называется плоскость, перпендикулярная к одной
из плоскостей проекций. Например, горизонтально-проецирующая плоскость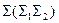перпендикулярна к горизонтальной плоскости проекции П₁ (рисунок 5.3).

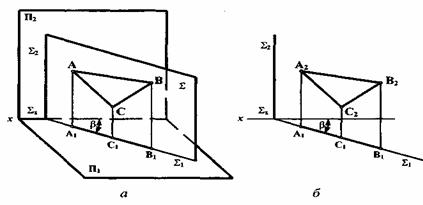
Рисунок 5.3

Горизонтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с горизон­тальным следом ₁. Угол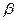, который образуется между плоскостями и П₂, проецируется на П₁ без искажения. Фронтальный след ₂ пер­пендикулярен к оси x.

Фронтально-проецирующая плоскость 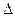(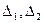) перпендикулярна к фронтальной плоскости П₂ показана на рисунке 5.4. Фронтальные проекции всех геометрических образов (точек, пря­мых, фигур), лежащих в этой плоскости, совпадают с фронтальным следом плоскости 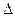₂. Угол 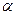, который образуется между заданной плоскостью 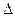и П₁, проецируется на П₂ без искажения. Горизонталь­ный след плоскости 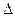₁ перпендикулярен к оси x.

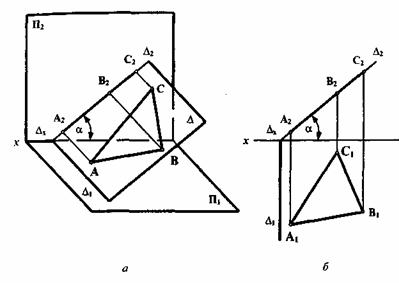
Рисунок 5.4

Профильно-проецирующая плоскость Т (T₁, T₂) перпендикулярна к профильной плоскости проекции П₃ (рисунок 5.5).

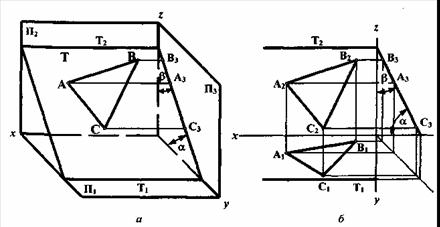
Рисунок 5.5

Профильные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с профильным следом плоскости Т₃. Углы 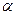и 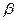, которые образуются между задан­ной плоскостью и плоскостями проекций П₁и П₂(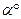= T^П₁; 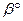= Т^П₂ ), проецируются на плоскость П₃без искажений. Горизон­тальный и фронтальный следы плоскости параллельны оси х.

Профильно-проецирующая плоскость может проходить через ось x: (рисунок 5.6).

Рисунок 5.6

Следы этой плоскости ₁ = ₂ совпадают друг с другом и с осью x, поэтому не определяют положение плоскости. Необходимо кроме следов задать в плоскости точку (рисунок 5.6). В частном случае эта плос­кость может быть биссекторной плоскостью. Угол 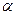° = °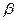, а точка А равноудалена от плоскостей проекций П₁и П₂. Плоскостью уровня называется плоскость, перпендикулярная од­новременно к двум плоскостям проекций и параллельная третьей. Та­ких плоскостей три разновидности (рисунок 5.7):

· горизонтальная плоскость уровня перпендикулярна к П₂, П₃ и параллельна П ₁ (рисунок 5.7, а);

· фронтальная плоскость уровня перпендикулярна к П₁,П₃ и па­раллельна П₂(рисунок 5.7, б);

· профильная плоскость уровня перпендикулярна к П₁, П₂ и параллельна П₃(рисунок 5.7 в).

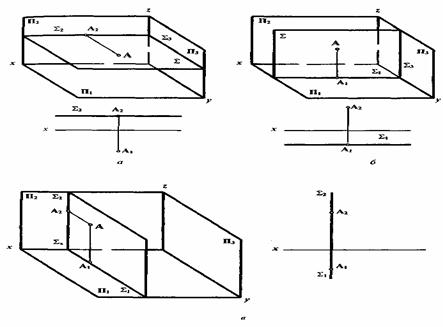
Рисунок 5.7

Из определения плоскостей уровня следует, что одна из проекций точки, линии, фигуры, принадлежащих этим плоскостям, будет совпадать с одноименным следом плоскости уровня, а другая проекция будет натуральной величиной этих геометрических образов.

5.4 Признаки принадлежности точки и прямой плоскости

Для определения принадлежности точки и прямой плоскости, расположенной в пространстве, следует руководствоваться следующими положениями:

· точка принадлежит плоскости, если через нее можно провести линию, лежащую в плоскости;

· прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки;

· прямая принадлежит плоскости, если она проходит через точку данной плоскости параллельно прямой, принадлежащей этой плоскости.

Через одну точку на плоскости можно провести бесконечное мно­жество линий. Это могут быть произвольные линии и линии, зани­мающие особое положение по отношению к плоскостям проекций П₁ П₂, П₃. Прямая, принадлежащая рассматриваемой плоскости, прове­денная параллельно горизонтальной плоскости проекций, называется г оризонталью плоскости.

Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно фронтальной плоскости проекций, называется фронталью плоскости.

Горизонталь и фронталь являются линиями уровня.

Горизонталь плоскости следует начинать строить с фронтальной проекции, т.к. она параллельна оси x, горизонтальная проекция гори­зонтали параллельна горизонтальному следу плоскости.

А так как все горизонтали плоскости параллельны между собой, можно считать горизонтальный след плоскости нулевой горизонталью (рисунок 5.8).

Фронталь плоскости следует начинать строить с горизонтальной проекции, т.к. она параллельна оси x, фронтальная проекция фронтали параллельна фронтальному следу. Фронтальный след плоскости - нулевая фронталь. Все фронтали плоскости параллельны между собой (рисунок 5.9).

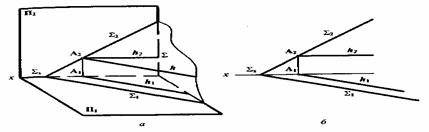
Рисунок 5.8

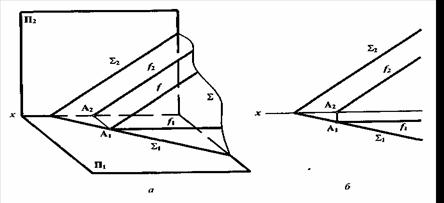
Рисунок 5.9

К линии уровня относится и профильная прямая, лежащая в за­данной плоскости и параллельная П₃.

К главным линиям особого положения в плоскости, кроме линии уровня, относятся линии наибольшего наклона плоскости к плоскости проекций.

5.5 Определение угла наклона плоскости к плоскостям проекций

Плоскость общего положения, расположенная в пространстве произвольно, наклонена к плоскостям проекций. Для определения величины двухгранного угла наклона заданной плоскости к какой-либо плоскости проекции используются линии наибольшего наклона плоскости к плоскости проекций: к П₁ - линия ската, к П₂ - линия наибольшего наклона плоскости к плоскости П₂.

Линии наибольшего наклона плоскости - это прямые, образующие с плоскостью проекций наибольший угол, проводятся в плоскости перпендикулярно к соответствующей линии уровня. Линии наибольшего наклона и ее соответствующая проекция образуют линейный угол, которым измеряется величина двухгранного угла, составленного данной плоскостью и плоскостью проекций (рисунок 5.10).

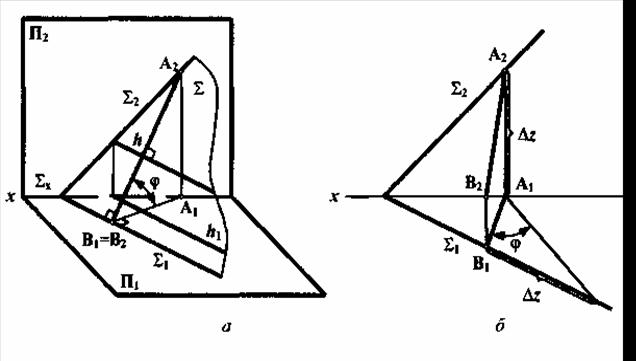
Рисунок 5.10

Дата добавления: 2014-01-06