Взаимное положение прямой линии и плоскости

Взаимное положение двух плоскостей

Две произвольные плоскости в пространстве по отношению друг к другу могут занимать два положения:

· плоскости пересекаются, при этом линия их пересечения всегда прямая;

· плоскости параллельны друг другу.

6.1 Условия пересечения плоскостей

Две произвольные плоскости в пространстве пересекаются по прямой линии. Как известно, две точки вполне определяют единст­венную прямую в пространстве. Следовательно, задача по построе­нию линии пересечения плоскостей сводится к определению положе­ния двух принадлежащих им обеим точек. Прямая пересечения плос­костей может быть построена и при условии, если определена одна общая для плоскостей точка и известно направление этой линии.

6.2 Условия параллельности плоскостей

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости:

· если плоскости заданы пересекающимися прямыми, то они будут параллельны в случае, когда одноименные проекции прямых, будут параллельны;

· если плоскости заданы линиями уровня (фронталями и горизон­талями), то они будут параллельны в случае, когда одноименные проекции линий уровня параллельны между собой;

· если плоскости заданы следами, то они параллельны тогда, когда параллельны их одноименные следы;

· если плоскости заданы любым другим способом, то в них необ­ходимо построить пересекающиеся прямые (общего положения, уровня или следы) и сравнить их одноименные проекции. Если плоскости параллельны, то одноименные проекции пересекающихся прямых взаимно параллельны.

7.1 Определение взаимного положения прямой линии и плоскости

Прямая линия и плоскость в пространстве относительно друг дру­га могут занимать следующие положения:

· прямая линия параллельна плоскости (частный случай — прямая лежит в плоскости);

· прямая линия пересекается с плоскостью (частный случай — прямая перпендикулярна к плоскости).

Иногда на чертеже нельзя непосредственно установить положение прямой линии т и плоскости (рисунок 7.1).

Рисунок 7.1

В этом случае прибегают к некоторым вспомогательным построе­ниям. В результате данных построений от вопроса о взаимном поло­жении прямой линии и плоскости переходят к вопросу о взаимном положении двух прямых линий. В задачах этого типа используют ме­тод вспомогательной плоскости. Заключается он в следующем:

- через данную прямую т проводят вспомогательную плоскость 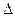. Подбор вспомогательной плоскости производится таким образом, чтобы решение задачи было наиболее простым;

· строят линию пересечения плоскостей - заданной и вспомогательной Δ;

· устанавливают взаимное положение прямой т и линии пересечения плоскостей п.

При этом возможны следующие случаи:

· прямая т параллельна прямой, следовательно, прямая т параллельна плоскости ;

· прямая т пересекает прямую, следовательно, прямая т пере­секает плоскость .

7.2 Пересечение прямой линии и плоскости

Если одна из пересекающихся фигур занимает проецирующее по­ложение, то точка пересечения находится значительно проще.

7.2.1 Задание:найти точку пересечения прямой m с проецирую­щей плоскостью (рисунок 7.2).

Рисунок 7.2

Решение:проанализировав чертеж, легко заметить, что плоскость занимает проецирующее положение (плоскость перпендикулярна к плоскости П₂.)

Сразу определяется фронтальная проекция К₂точки пересечения прямой m с плоскостью Σ. Горизонтальная проекция K ₁ искомой точки находится с помощью линии связи на горизонтальной проекции прямой т₁. На плоскость П₂плоскость проецируется в линию, сов­падающую с фронтальным следом ₂, значит, прямая видима по обе стороны от следа ₂.

При определении видимости прямой на горизонтальной проекции необходимо установить, какой участок прямой находится над плоско­стью , т.е. будет видимым на горизонтальной проекции. Таким уча­стком является луч, расположенный левее точки К.

7.2.2 Задание:найти точку пересечения проецирующей прямой т с плоскостью (АВС) (рисунок 7.3).

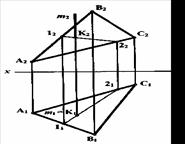
Рисунок 7.3

Решение: из чертежа видно, что плоскость, заданная треугольни­ком ABC, занимает общее положение относительно плоскостей про­екции, прямая т является горизонтально проецирующей, т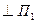. Сразу определяется горизонтальная проекция k₁искомой точки пере­сечения прямой т с плоскостью . Для нахождения фронтальной про­екции К₂ точки в плоскости треугольника ABC проводится вспомога­тельная прямая 1-2. В пересечении её фронтальной проекции 1₁-2₂ с фронтальной проекцией прямой т находят фронтальную проекцию К₂ искомой точки К.

7.2.3 Задание: найти точку пересечения прямой т общего поло­жения с плоскостью общего положения (ABC) (рисунок 7.4).

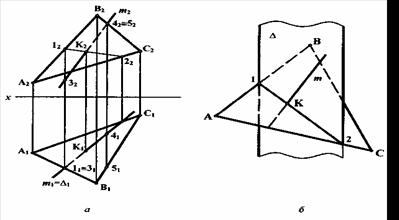
Рисунок 7.4

Решение:в данной задаче прямая т и плоскость занимают об­щее положение относительно плоскостей проекций. Задача решается по следующей схеме:

· через прямую т проводят вспомогательную плоскость 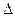. В данной задаче , то есть является горизонтально проецирующей;

· находят линию 1-2 пересечения плоскостей (АВС) и ;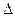

· определяют точку К пересечения прямой т с плоскостью в пе­ресечении прямых 1-2 и т.

Видимость прямой т относительно плоскости S определяется с помощью конкурирующих точек.

Для определения видимости на горизонтальной проекции выбира­ется пара точек 1 и 3. У этих точек координаты у одинаковы (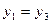), координаты z различны (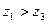), точка 1 выше точки 3.

Следовательно, на горизонтальной проекции левее точки k₁ пря­мая т находится под плоскостью треугольника ABC, то есть должна быть проведена штриховой линией.

Для определения видимости на фронтальной проекции можно воспользоваться парой точек 4 и 5 и рассмотреть их аналогично паре точек 1 и 3.

7.3 Параллельность прямой и плоскости

Прямая и плоскость параллельны, если в плоскости имеется пря­мая, параллельная заданной прямой.

7.3.1 Задание:построить проекции прямой, проходящей через точку А и параллельной прямой т, принадлежащей плоскости (BCD) (рис. 7.5).

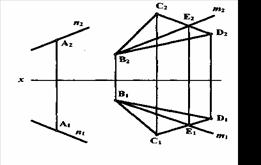
Рисунок 7.5

Решение:в условии задачи задана фронтальная проекция m₂ пря­мой m. Поэтому необходимо вначале найти горизонтальную проек­цию m₁ прямой m. Условия параллельности прямой и плоскости: пря­мая параллельна плоскости, если она параллельна какой-то прямой, расположенной в данной плоскости.

Используя это условие, строят проекции искомой прямой, прохо­дящие через точку А; п₁ проводится параллельно т₁, n₂ — параллель­но m_2.

Дата добавления: 2014-01-06