Построение линии пересечения поверхностей

Предложенные в настоящей работе задания охватывают задачи не на все методы построения линий пересечения поверхностей, а только наиболее распространенные.

Ниже приведены решения типовых задач, когда применены раз­личные способы в зависимости от формы и расположения пересе­кающихся поверхностей.

13.1 Одна из поверхностей занимает частное (проецирующее) положение

13.1.1 Задание:даны две поверхности: - тора и Р - цилиндра (рисунок 13.1). Требуется построить линию их пересечения.

Решение:поверхность цилиндра перпендикулярна к П₂, следова­тельно, она проецирующая. В таком случае фронтальная проекция линии пересечения уже известна. Она совпадает с фронтальной про­екцией цилиндра. Решение задачи, т.е. построение горизонтальной проекции линии пересечения, сводится к нахождению второй проек­ции линии, принадлежащей поверхности . Для достижения этой цели на фронтальной проекции фиксируют опорные (1, 2, 4, 9) и промежу­точные точки и находят их положения на горизонтальной проекции (рисунок 13.2).

Ниже приводится построение горизонтальной проекции только одной точки 1 (рисунок 13.1). Из этой точки вниз проводят линию проек­ционной связи. Одновременно из этой же точки радиусом 01₂ прово­дят дугу окружности, на которой лежит эта точка, как принадлежащая тору, и находят проекцию этой окружности на горизонтальной проек­ции тора - это прямая линия, параллельная оси x. Она проходит через точку l₁ (точка пересечения окружности, проходящей через точку 1, с окружностью тора, лежащей на П₁). Горизонтальная проекция точки 1 находится на пересечении линии проекционной связи, проведенной из точки 1₂, с горизонтальной проекцией окружности тора, на которой лежит точка 1. Остальные точки строят аналогично точке 1 (рисунок 13.2).

Точки 4 и 9 определяют видимость линии пересечения на гори­зонтальной проекции, а точки 1 и 2 наиболее удаленные от контура на горизонтальной проекции.

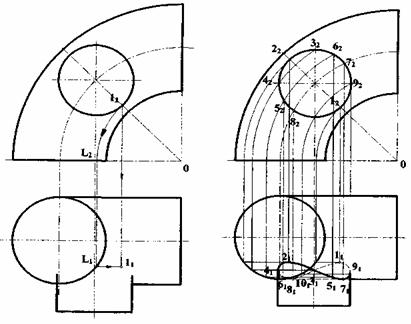
Рисунок 13.1 Рисунок 13.2

Эту задачу можно решать и методом вспомогательных секущих плоскостей, который рассматривается в следующем пункте.

13.2 Метод вспомогательных секущих плоскостей

Этот метод применяется для построения линии пересечения двух поверхностей, когда секущие (параллельные) плоскости при пересе­чении с данными поверхностями образуют простые линии (прямую или окружность).

13.2.1 Задание:даны поверхности конуса и цилиндра ф (рисунок 13.3). Требуется построить линию их пересечения.

Решение:ось цилиндра перпендикулярна к плоскости П₂, следо­вательно, поверхность цилиндра - проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (пункт 13.1.1) примере. Для этого определяют опорные - наивысшую и низшую точки 1 и 2, которые лежат на пересечении фронтальной про­екции цилиндра с очерковой образующей конуса. Их горизонтальные проекции 1₁ и 2₁ принадлежат горизонтальной проекции очерковой образующей конуса (l₁ и 2₁, совпадают с осевой линией конуса). Точ­ки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции. Для определения их горизонтальных проекций через ось цилиндра параллельно П₁проводят вспомогательную секущую плос­кость Г (ее фронтальный след Г₂). Эта плоскость рассечет цилиндр по очерковым образующим, а конус по окружности радиусом R, которая на П₁будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции опорных точек 3₁ к 4₁ (рисунок 13.3).

Построение промежуточных точек аналогично построению то­чек 3 и 4, только образующие, по которым вспомогательная плоскость будет рассекать цилиндр, не будут очерковыми (рисунок 13.4).

Рисунок 13.3 Рисунок 13.4

13.3 Метод вспомогательных концентрических сфер

Этот метод применяется для построения линии пересечения двух поверхностей вращения, когда их оси пересекаются и параллельны плоскости проекции. Точка пересечения осей принимается за центр вспомогательных концентрических секущих сфер.

13.3.1 Задание:Даны две поверхности вращения - конус и ци­линдр, оси которых пересекаются и находятся в одной плоскости, па­раллельной П₂(рисунок 13.5). Требуется построить линию их пересече­ния.

Решение:на фронтальной проекции фиксируют точки пересече­ния меридианов заданных поверхностей вращения 1₂ и 2₂ - они при­надлежат искомой линии пересечения. Горизонтальные проекции этих точек находятся на осевой линии конуса и цилиндра - 1, и 2,. Другие точки линии пересечения можно построить, используя кон­центрические сферические посредники, как вспомогательные секущие поверхности. Из точки пересечения осей фронтальных проекций, как из центра, проводятся сферы. Первая - касательная к проекции кону­са, а последующие - большим радиусом (рисунок 13.6).

Рисунок 13.5 Рисунок 13.6

Каждая сфера пересекает обе поверхности по окружностям, фрон­тальные проекции которых изображаются отрезками прямых линий. Эти проекции пересекаются в точках, являющихся фронтальными проекциями точек искомой линии пересечения поверхностей.

Горизонтальные проекции этих точек определяются по принад­лежности одной из поверхностей. В данном случае удобнее их полу­чать по принадлежности конусу. Например, точки 3 и 4 лежат на той же окружности, по которой вспомогательная сфера пересекает конус. Изменяя радиус вспомогательной секущей сферы, находят последова­тельный ряд точек линии пересечения, соединив которые, получают проекции искомой линии (рисунок 13.6). Чтобы определить видимость го­ризонтальной проекции линии пересечения, на её фронтальной про­екции отмечают точки, лежащие на осевой линии цилиндра и принад­лежащие линии пересечения. Затем по линиям проекционной связи переносят их на очерковые образующие горизонтальной проекции цилиндра. Точки, лежащие ниже указанных точек, будут находиться на не­видимой части цилиндра.

13.4 Метод эксцентрических сфер

Метод эксцентрических сфер применяется для построения линии пересечении поверхностей вращения, у которых оси расположены в одной плоскости, являющейся плоскостью симметрии. При этом пе­ресекающиеся поверхности должны иметь семейство круговых сече­ний.

13.4.1 Задание:даны две поверхности вращения - тор и конус, оси которых находятся в одной плоскости, параллельной П₁ (рисунок 13.7). Требуется построить линии их пересечения.

Решение:прежде всего, фиксируют опорные точки пересечения очерковых меридианов 1 и 2. Затем через ось вращения поверхности кольца проводят фронтальный след ₂ фронтально проецирующей плоскости . Линия пересечения её с поверхностью тора - окруж­ность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомо­гательной секущей сферой по окружности, её центр должен находить­ся на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса (O₂) выбирается центром вспомогатель­ной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости 1.2- Такая вспомога­тельная секущая сфера пересекает кольцо и конус вращения по ок­ружностям, фронтальные проекции которых - отрезки прямых. Точка пресечения этих отрезков 3₂ (рисунок 13.7) принадлежит искомой линии пересечения поверхностей.

Вспомогательные сферы имеют различные центры на оси конуса вращения; так, при построении проекции - точки 4₂ - О'₂. Горизон­тальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, кону­са.

Рисунок 13.7

Литература

1. Арустамов Х.А. Сборник задач по начертательной геометрии. -М.: Машиностроение, 1978. -445 с.

2. Гордон В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский. — М.: Высшая школа, 2000. — 272 с.

3. Гордон В.О. Сборник задач по курсу «Начертательная геомет­рия» / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева. - М.: Высшая школа,2000.

4. Чекмарев А.А. Инженерная графика. - М.: Высшая школа, 1998.-365с.

5. Фролов С.А.Начертательная геометрия.-М.:Высшая школа,1983.-240 с.

Бурменко Ф.Ю., Ени В.В., Лупашко Г.П.,

Дата добавления: 2014-01-06