Доказательство

Если (Х;У)- дискретная двумерная случайная величина, причем Х и У независимые случайные величины, то

k_xy= M[(X-m_x)(Y-m_y)]= ½т.к. X и Y независимые случайные величины, то p_ij=p_ip_j ½=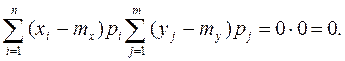g

Аналогично проводится доказательство, если (Х;У)- непрерывная двумерная случайная величина.

Заметим, что из некоррелированности случайных величин, в общем случае, еще не следует их независимость. Можно построить примеры таких случайных величин, которые являются некоррелированными, но зависимыми.

Итак:

· из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность.

· Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

Числа k_xy и r_xy характеризуют не всякую зависимость, а только так называемую линейную зависимость между случайными величинами Х и У. Некоррелированность эквивалентна линейной независимости.

Отметим на плоскости в системе координат точками результаты измерений случайной величины (Х;У).

Рис.11

Ограничимся приближенным представлением (точное приближение, вообще говоря невозможно) величины Y в виде линейной функции величины X.

у

Найдем линейную зависимость у=kx+b (графиком которой является прямая), которая давала бы возможность предсказывать как можно точнее значения случайной величины У по значениям случайной величины Х, т.е. такую линейную зависимость, чтобы ошибка предсказания M[(Y-y)²], была минимальной.

Можно доказать, что в этом случае

k = 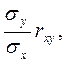b = m_y - km_x.

При этих значениях k и b прямая y=kx+b имеет вид

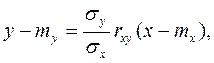
и называется прямой среднеквадратической регрессии У на Х, где 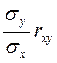называется коэффициентом регрессии Y на X.

При этом ошибка замены равна

M[(Y-(kx+b))²]=.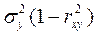

Тогда найдем,==.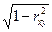

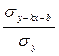Отсюда видно, что -1£ r_xy£ 1 (т.к. 1-r²_xy³ 0) и чем ближе r²_xy к единице, тем теснее линейная зависимость между случайными величинами Х и У, если же r_xy=±1, то Х и У связаны линейной зависимостью Y=kX+b с вероятностью единица.

Аналогично можно получить прямую среднеквадратической регрессии X на Y:

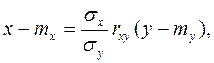
где 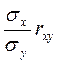- коэффициент регрессии X на Y.

Если r_xy= ±1, то обе прямые регрессии, как очевидно, совпадают. Из уравнений прямых регрессии следует, что обе прямые регрессии проходят через точку (m_x,m_y), которую называют центром совместного распределения величин X и Y.

Дата добавления: 2014-01-06