Примитивно-рекурсивные функции

Лекция № 4. Рекурсивные функции

1. Примитивно-рекурсивные функции

2. Частично-рекурсивные и общерекурсивные функции

С.К.Клини

Формализация понятия алгоритма в терминах рекурсивных функций предложена в 1936 году в работах А.Черча (общерекурсивные функции) и работах С.К.Клини (частично рекурсивные функции, 1938).

А.Черч

Функция непосредственно следующее натуральное число, обозначаемая штрихом, позволяет по числу 0 построить любой начальный отрезок множества натуральных чисел. Обозначения при этом таковы: 0, 0^/=1, 0^//=1^/,=2, …

Функции выбора аргумента определяются равенствами:

W_k(x₁,x₂, x_k,…, x_n)=x_k (1£k£n).

Функция непосредственно следующее натуральное число, и функции выбора аргумента образуют так называемое множество базисных функций. Функции, входящие в это множество всюду определены на множестве натуральных чисел.

Говорят, что функция может быть построена при применении оператора суперпозиции к функциямнескольких переменных, если она может быть определена в результате следующих действий:

1) подстановки функции в функцию;

2) переименовывания переменных;

3) отождествления переменных;

4) исключения переменных замещением их константами.

Пример 4.1.1. Даны функции g(y₁,y₂), w(x₁, x₂, x₃). Говорят, что функция f(x₁, y₁, y₂, x₃)=w(x₁, g(y₁,y₂), x₃) построена путем подстановки функции g(y₁,y₂) в функцию w(x₁, x₂, x₃).

Пример 4.1.2. Даны функции g(t), w(x₁, x₂, x₃). Говорят, что функция f(x₁,t,x₃)=w(x₁, g(t), x₃) построена путем переименовывания переменных.

Пример 4.1.3. Даны функции g₁(t), g₂(t), w(x₁, x₂, x₃). Говорят, что функция f(x₁,t)=w(x₁, g₁(t), g₂(t)) построена путем отождествления переменных.

Пример 4.1.4. Дана функция w(x₁, x₂, x₃). Говорят, что функция f(x₁,x₃)= w(x₁, m, x₃) построена путем исключения переменных замещением их константами.

Оператор примитивной рекурсии применяется к двум функциям n-1 и n+1 переменных для построения функции n переменных.

Определяющие соотношения оператора примитивной рекурсии записываются так.

1. При n=1 по натуральному числу m и функции двух переменных h(u,v) строится функция одной переменной f(y):

.

2. При n>1 по заданным функциям q(x₁, x₂, …, x_n-1) и h(x₁, x₂, …, x_n+1) строится функция n переменных f(x₁, x₂,, x_n–1, x_n):

.

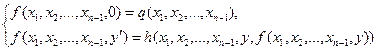Определение 4.1.1. Функция называется примитивно рекурсивной, если она есть базисная функция или может быть построена исходя из базисных функций конечным числом применений операторов суперпозиции и примитивной рекурсии.

Пример 4.1.5. Функция g(x)=x – базисная. Функция h(x₁, x₂, x₃)=x₃ ^/ может быть получена применением оператора суперпозиции двух базисных функций x₃ ^/ и w(x₁, x₂, x₃)=x₃. Исходя из функций g(x)=x, h(x₁, x₂, x₃) построим функцию двух переменных f(x,y) с применением оператора примитивной рекурсии:

Таким образом, согласно определению эта функция является примитивно рекурсивной. В то же время, исходя из определения функции h(x₁,x₂,x₃) запись функции f(x,y) можно сделать более наглядной:

Или совсем простой – f(x,y)=x+y.

Последнее утверждение проверяется просто:

f(x,0)=x+0=x, f(x,y+1)=x+(y+1)=(x+y)+1= f(x,y)+1=(f(x,y))^/.

Фактически в примере 5 мы доказали примитивную рекурсивность функции f(x,y)=x+y.

Аналогично доказывается примитивная рекурсивность функций:

,

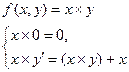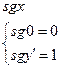
А также функций f(x,y)=x^y, f(x)=x!.

Определение 4.1.2. Транзитивное замыкание множества базисных функций относительно операторов суперпозиции функций и примитивной рекурсии называется классом примитивно рекурсивных функций.

Определение 4.1.3. Говорят, что функция f(x₁,x,₂,…x_n) получена из функций g(x₁,x,₂,…x_n, z) и a(x₁,x,₂,…x_n) с помощью ограниченного оператора минимизации (ограниченного m-оператора) и обозначают:

f(x₁,x,₂,…x_n)= m z£a [ g(x₁,x,₂,…x_n, z)= 0],

если f(x₁,x,₂,…x_n)= z£a(x₁,x,₂,…x_n)

тогда и только тогда, когда:

g(x₁,x,₂,…x_n, k)¹0 при k =0, 1, 2, … z–1, и g(x₁,x,₂,…x_n, z)= 0.

Теорема 4.1.3. Применение ограниченного m- оператора не выводит из класса примитивно рекурсивных функций.

Дата добавления: 2014-01-06