Мода и медиана. Моменты случайных величин. Асимметрия и эксцесс. Квантили

X

обознача­ется через M_OX.

н.с.b. M₀X — точка максимума (локального) плотности f_x(x).

Рис. 23

М_еХ X х_р

Р{Х < х_р} = Р{Х > х_р} =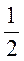, (46)

св. X k- α_к.

Таким образом, по определению

α_к = М(Х^к) (47)

Для д. с. в. начальный момент выражается суммой:

α_к = 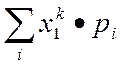(48)

а для н. с. в. — интегралом:

α_к = (49)

В частности, α₁=MX, т.е. начальный момент 1-го порядка есть математическое ожидание.

k с. в. X (X — МХ)^k, обозначается через μ_k.

Таким образом, по определению

μ_к = М(Х - МХ)^k (50)

В частности, μ₂=DX, т.е. центральный момент 2-го порядка есть дисперсия.

Для д. с. в.:

μ_к = (51)

а для н. с. в.:

μ_к= 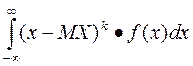(52)

Центральные моменты могут быть выражены через начальные моменты. Так. Μ₂ = DX = α₂— α₁² (действительно: μ₂ = DX = MX² — (MX)² = α₂ — α₁²); μ₃= α₃ — 3 α₁ α₂ + 2 α₁³, μ₄ = α₄ - 4 α₁ α₃ + 6 α₁² α₂ — 3 α₁⁴ и т. д.

Коэффициентом асимметрии («скошенности») A с.в. X называ­ется величина

А= ( 53)

Если А > 0, то кривая распределения более полога справа от M_оX (рис. 24).

Если А < 0, то кривая распределения более полога слева от M_оX (рис. 25).

Коэффициентом эксцесса («островершинности») Е с. в. X назы­вается величина

E= (54)

Для нормального закона распределения А = 0 и Е = 0; остальные распределения сравниваются с нор­мальным: если Е > 0 — более островершинные, а распределения «плос­ковершинные» имеют Е < 0 (рис. 26).

Квантилью уровня р с. в. X называется решение уравнения

F_X(x _P) =p (55)

где р — некоторое число, 0 < р < 1.

Квантили x _0,25, x _0,5 и x _0,75 имеют свои названия: нижняя кван­тиль, медиана (М_еХ = x _0,5), верхняя квантиль соответственно. Они делят числовую прямую на 4 части, вероятности попадания в которые равны 0, 25 (рис. 27).

Глава3 Выборки и их характеристики

Дата добавления: 2014-01-06