Ранжирование

Статистическое распределение выборки.

Предмет математической статистики

23. Генеральная и выборочная совокупности

генеральная совокупность — это с. в. Х(ω), заданная на пространстве элементарных событий Ώ, с выделенным в нем классом S подмножеств событий, для которых указаны их вероятности.

выборка — это последовательность Х₁, Х₂,…, Х_n независимых одинаково распределенных с.в., распределение каждой из которых совпадает с распределением генеральной случайной величины.

х₁, х₂,…,х_п.

репрезентативной

Пример1. Десять абитуриентов проходят тестирование по матема­тике. Каждый из них может набрать от 0 до 5 баллов включительно. Пусть X_k — количество баллов, набранных k-м (к = 1,2,..., 10) аби­туриентом.

Тогда значения 0, 1, 2, 3, 4, 5 — все возможные количества бал­лов, набранных одним абитуриентом, — образуют генеральную сово­купность.

Выборка Х₁,Х₂,…, Х₁₀ — результат тестирования 10 абитури­ентов.

Реализациями выборки могут быть следующие наборы чисел: {5, 3, 0, 1, 4, 2, 5, 4, 1, 5} или {4, 4, 5, 3, 3, 1, 5, 5, 2, 5} или {3, 4, 5, 0, 1, 2, 3, 4, 5, 4} и т.д.

Эмпирическая функция распределения.

св. X.

Пусть она приняла n₁ раз значение x₁,

n₂ раз — значение x₂,

…,

n_k раз — значение x_k.

При этом n₁ + n₂ +…+ n_k =n— объем выборки. Значения x₁, x₂, …, x_k называют вариантами св. X.

Полученная таким образом последовательность

x ₍₁₎, x ₍₂₎, …, x _(n) (где x ₍₁₎ £ x ₍₂₎ £ …£ x _(n) и x ₍₁₎ =,…, x _(n) =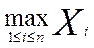) называется вариационным рядом.

Числа n_i, x_i

р _i *-частности (56), где n=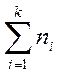

Пример 2. В результате тестирования (см. пример 6.1) группа аби­туриентов набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку в виде: а) вариационного ряда; б) статистического ряда.

а) Проранжировав статистические данные (т. е. исходный ряд), получим вариационный ряд (x ₍₁₎, x ₍₂₎, …, x ₍₁₀₎):

(0, 1, 1, 2, 3, 4, 4, 5, 5, 5).

б) Подсчитав частоту и частость вариантов x ₁ =0, x ₂ =1, x ₃ =2, x ₄ =3, x ₅ = 4, x ₆ =5, получим статистическое распределение выборки) (так называемый дискретный статистический ряд)

x i
ni

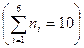
или

x i
рi*

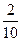
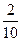
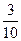
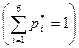
Статистическое распределение выборки является оценкой неизвестного распределения.

р_i* n → ∞ р_i, р_i*р_i. n

[x₀, x₁), [x₁, x₂), …, [x_k-1, x_k),

h = x₁ – x₀ = х₂ — x₁ =....

Для определения величины интервала (h) можно использовать формулу Стерджеса:

(57)

где х_mах—x_min — разность между наибольшим и наименьшим значени­ями признака, m= 1 + log₂ n — число интервалов (log₂ n ≈ 3,322 lg n). За начало первого интервала рекомендуется брать величину x_нач = x_min—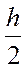. Во второй строчке статистического ряда вписывают количество наблюдений n_i (i =1,…,k), попавших в каждый интервал.

Пример 3. Измерили рост (с точностью до см) 30 наудачу отобран­ных студентов. Результаты измерений таковы:

178, 160, 154, 183, 155, 153, 167, 186, 163, 155,

157, 175, 170, 166, 159, 173, 182, 167, 171, 169,

179, 165, 156, 179, 158, 171, 175, 173, 164, 172.

Построить интервальный статистический ряд.

Для удобства проранжируем полученные данные:

153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165. 166. 167, 167, 169, 170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.

Отметим, что X — рост студента — непрерывная с. в. При более точном измерении роста значения с. в. X обычно не повторяются (веро­ятность наличия на Земле двух человек, рост которых равен, скажем 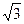= 1,732050808... метров, равна нулю!).

х_тiп = 153, х_mах = 186; по формуле Стерджеса, при п = 30, находим длину частичного интервала

h = 6. Тогда х_нач = 153-= 150. Исходные данные

разбиваем на 6 (т = 1 + log₂30 = 5,907 ≈ 6) интервалов: [150,156), [156,162), [162,168), [168,174), [174, 180), [180, 186).

Подсчитав число студентов (n_i), попавших в каждый из полученных промежутков, получим интервальный статистический ряд:

Рост	[150-156)	[156-162)	[162-168)	[168-174)	[174-180)	[180-186)
Частота
Частость	0,13	0,17	0,20	0,23	0,17	0,10

Эмпирической (статистической) функцией распределения называется функция F_n* (х), определяющая для каждого значения х частость события {X < х}:

F_n* (х)=p*{X<x}. (58)

Для нахождения значений эмпирической функции удобно F_n* (х) писать в виде

F_n* (х)=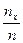 (59), где n — объем выборки, n_х — число наблюдений, меньших x (x Î R)

п события {X < х}

F_n* (х) является оценкой вероятности события {X < х}

Теорема1. (Гливенко). Пусть F(x) — теоретическая функция рас­пределения с.в. X, а F_n* (х) — эмпирическая. Тогда для любого e > 0

lim { |F_n*(х) - F(x)|>e} = 0.

Пример 4. Построить функцию F_n* (х), используя условие и результаты примера 2.

Здесь п = 10. Имеем F*₁₀(x) = 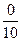= 0 при х£ 0 (наблюдений меньше 0 нет); F*₁₀(x) = при 0 < х£ 1 (здесь

x i
рi*

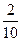
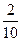
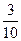
n_х=1) и т. д. Окончательно получаем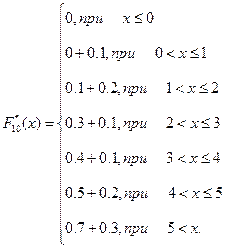

График эмпирической функции распределения приведен на рис.

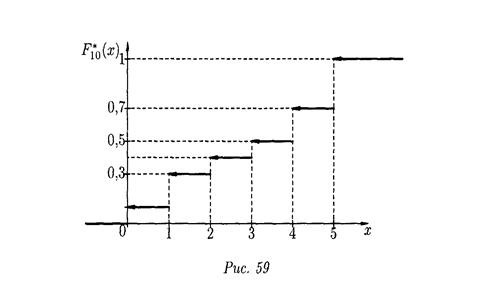
Дата добавления: 2014-01-06