
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числовые характеристики статистического распределения
|
|
|
|
n
| xi | x1 | x2 | x3 | … | xk |
| ni | n1 | n2 | n3 | … | nk |
Выборочным средним 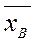 называется среднее арифметическое всех значений выборки:
называется среднее арифметическое всех значений выборки:
 (60)
(60)
или
 (61), где p*i =
(61), где p*i = — частость.
— частость.
xi ni
Выборочной дисперсией DB называется среднее арифметическое квадратов отклонений значений выборки от выборочной средней  т.е.
т.е.
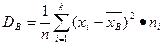 (62)
(62)
Или
 (63)
(63)
Выборочное среднее квадратическое отклонение выборки определяется формулой
 (64)
(64)
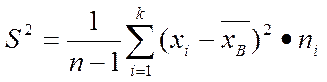 (65)
(65)
или
 (66)
(66)
исправленной выборочной дисперсией
Величина
 (67)
(67)
называется исправленным выборочным средним квадратическим отклонением.
х1, х2,…, хk
[ х0, х1 ), [ х1, х2 ), …,
а их середины 
 ….
….
x(1), x(2), …, x(n) используется медиана, мода, размах вариации (выборки).
Размахом вариации называется число R = x(n) — x(1), где x(1) =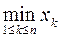 , x(n) =
, x(n) = 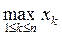 или R = xmax—xmin (68), где xmах — наибольший, xmin — наименьший вариант ряда.
или R = xmax—xmin (68), где xmах — наибольший, xmin — наименьший вариант ряда.
Модой М0* вариационного ряда называется вариант, имеющий наибольшую частоту.
Медианой Мe* вариационного ряда называется значение признака (св. X), приходящееся на середину ряда.
Если п = 2k (т. е. ряд x(1), x(2),…, x(k), x(k+1),..., x(2k), имеет четное число членов), то Мe* = 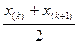 (69); если п = 2к + 1, то Мe* = x(k+1) (70)
(69); если п = 2к + 1, то Мe* = x(k+1) (70)
Пример 7. По условию примера - результаты тестирования 10 абитуриентов - найти характеристики выборки.
| x i | ||||||
| ni |
Используя формулы и определения из рассмотренного пункта, находим:
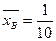 (0 • 1 + 1 • 2 +2•1+3•1+4•2+ 5 • 3) = 3,
(0 • 1 + 1 • 2 +2•1+3•1+4•2+ 5 • 3) = 3,
DB =  ((0 - 3)2 • 1 + (1 - 3)2 • 2 +(2-3) 2 •1+(3-3) 2•1+(4-3) 2 •2 + (5 - 3)2 • 3) = 3.2,
((0 - 3)2 • 1 + (1 - 3)2 • 2 +(2-3) 2 •1+(3-3) 2•1+(4-3) 2 •2 + (5 - 3)2 • 3) = 3.2,
sB = 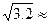 1.79,
1.79,
S2 =  • 3,2≈3.56.
• 3,2≈3.56.
S = 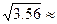 1,87,
1,87,
R = 5 -0 = 5,
М0* = 5,
Мe*= =3.5.
=3.5.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 410; Нарушение авторских прав?; Мы поможем в написании вашей работы!