Мощность двигателя

Тема: СИЛА ТЯГИ ДЛЯ ПЕРЕМЕЩЕНИЯ ГРУЗОВ

Лекция №5

Вопросы для рассмотрения:

1. Мощность двигателя.
2. Проверка прочности тяговых органов.
3. Диаграмма натяжения гибкого тягового органа.

Раздаточный материал:

1. Нагрузочные диаграммы двигателей

2. Диаграмма натяжений гибкого тягового органа

Рассмотрим равновесие системы приводной блок – редуктор – двигатель, приведя предварительно все силы к окружности приводного блока (барабана, звездочки, шкива трения) (рис. 5.3, д): 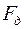– тяговое усилие двигателя; Р – сила инерции привода; 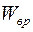– вредное сопротивление в самом приводе (жесткость тягового органа, трение в подшипниках приводного блока, трение в редукторе); 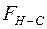– тяговое усилие. Последнее на приводной блок действует в направлении, обратном по отношению к направлению его действия на тяговый орган (рис. 5.3, д). Из условия равновесия приводного блока

,

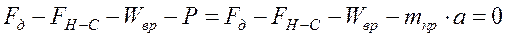откуда

, н, (5.17)

где а – ускорение тягового органа, м/с²; 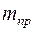– масса всех движущихся частей установки, приведенная к окружности блока, кг.

Учтем 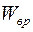с помощью к.п.д. привода. При положительном 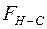, когда энергия передается от двигателя к приводному блоку, из (5.17) имеем:

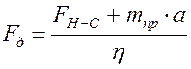, (5.18)

при отрицательном 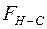, когда энергия передается от приводного блока к двигателю

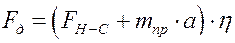, (5.19)

где – полный к.п.д. приводной станции, учитывающий потери на приводных блоках и в редукторе.

Механическая мощность двигателя в данный момент времени

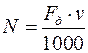, квт, (5.20)

где 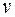– окружная скорость блока, м/с.

Для привода стационарных установок используют, как правило, электродвигатели асинхронные и реже синхронные. Двигатель выбирают по нагреву и рассчитывают по формуле

квт (5.21)

где 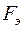– эквивалентное тяговое усилие двигателя, т.е. такое постоянное усилие, при котором двигатель нагреется до такой же температуры, как и при действительных значениях тяговых усилий (могут быть постоянными и переменными) за одинаковое время работы.

– номинальная скорость движения тягового органа, м/с.

Методы расчета 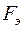и зависят от вида режима работы двигателя (рис. 5.4). Различают: 1) длительный циклический режим, когда в течение цикла работы (например канатная откатка) тяговые усилия на блоке меняются во времени, и 2) длительный с постоянной нагрузкой, которая не изменяется вообще или изменяется незначительно достаточно длительное время, за которое температура нагрева стабилизуется.

Рис. 5.4. Нагрузочные диаграммы двигателей

В первом случае, аналогично выше изложенному, обозначим через 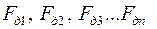– силы тяги за цикл, а через 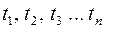– время их действия.

Тогда эквивалентное усилие двигателя определяют как среднеквадратичное за цикл нагрузки (период, после которого цикл нагрузки повторяется):

, н (5.22)

Здесь – суммарная продолжительность остановок за цикл, с. 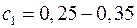– коэффициент, учитывающий ухудшение охлаждения двигателя с самовентиляцией при остановке (для двиг. с незавимой вентиляцией ).

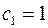По рассчитанной мощности выбирают ближайший двигатель по каталогу. Мощность установленного двигателя (выбранного) 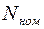называют его номинальной (установленной) мощностью. Выбранный двигатель проверяют на перегрузочную способность.

Для этого из известных уже значений выбирается (или определяется отдельно) максимальное значение и вычисляется из мощности формулы номинальное значение силы тяги

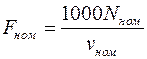, н (5.23)

Необходимая кратность момента двигателя

. (5.24)

Если взято для периода пуска, то по формуле (5.24) находится необходимая кратность пускового момента; если имеет место при установившемся режиме, то 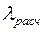определяет кратность максимального (опрокидывающего) момента двигателя. Сравнивая значения , полученные расчетом со значениями, указанными в паспорте двигателя, принимается решение о правильности выбранного двигателя. Если 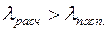, принимают следующий по мощности двигатель и снова проверяют его на перегрузочную способность.

Во втором случае (режим характерен для конвейеров) 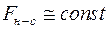. Мощность рассчитывается по формуле:

, квт (тягов. режим) (5.25)

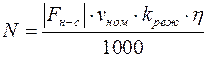, квт (тормозной режим) (5.26)

Здесь – коэффициент режима 1,2 – 0,8.

Если при определении сила инерции не учтена, выбранный двигатель проверяют на перегруз. способность для режима пуска.

5.5. Проверка прочности тяговых органов.

При эксплуатационных расчетах детали чаще всего рассчитывают по установившимся (статическим), реже по предельным (пиковым) нагрузкам. Проверка – определение запаса прочности 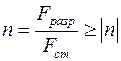, где – разрушающее усилие тягового органа, 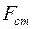– его максимальное статическое натяжение, 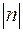– норматив запаса прочности. Если вместо 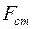принять – предельная пиковая нагрузка, то должен быть и соответствующий норматив запаса прочности . Чаще всего 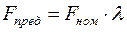, где – кратность макс. момента двигателя или предохранительной муфты.

5.6. Диаграмма натяжения гибкого тягового органа.

Одной из особенностей гибкого тягового органа (лента, цепь, канат) есть способность воспринимать только растягивающие усилия. При любых вариантах работы такой машины тяговый орган только растянут или усилие в каком-либо сечении может быть равно нулю. Поэтому пользуются термином (словом) натяжение тягового органа – это усилие, приходящееся на всю площадь поперечного сечения, измеряемое в ньютонах (не путать со словом напряжение – усилие, приходящееся на единицу площади поперечного сечения, измеряется в н/м², н/см², н/мм²). Расчеты транспортных установок включают определения величин натяжений, тягового органа в различных (по необходимости) сечениях, как правило в характерных сечениях, например, где изменяется траектория движения. При этом удобно пользоваться диаграммой натяжений гибкого тягового органа, особенно при замкнутых контурах (конвейеры), т.к. она, во-первых дает наглядную картину распределения натяжений по всему контуру и, во-вторых позволяет без дополнительных расчетов определять величину натяжения в любом сечении контура.

Построение диаграммы натяжений выполняется в такой последовательности:

– вычерчивается схема контура тягового органа (см. рис. 5.5, а), где обозначаются направление движения, нумеруються характерные точки (удобнее всего точкой 1 обозначить сечение сбегающей с привода ветви в месте изменения траектории, а далее – по ходу тягового органа);

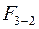– определяются величины сил тяги на всех участках контура – холостая ветвь; – ведомый барабан; 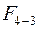– груженая ветвь;

– выбирается масштаб сил и масштаб длин в зависимости от размеров диаграммы, которую собираются строить.

Диаграмма натяжения строится в прямоугольной системе координат. По оси ординат откладываются силы, а по оси абсцисс – длина контура. Отличается порядок построения от обычного (когда вычеркиваются сначала координатные оси, а затем – величины) тем, что положение оси 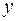вычерчивается сразу, а оси – находится в конце построения диаграммы.

Для изображенной на рис. 5.5, а, схемы, диаграмма включает три вертикальные линии (рис. 5.5, б) с одинаковыми промежутками, изображающими в масштабе длину каждой ветви схемы (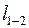и ). Линии нумеруются слева направо. Средняя линия имеет два номера, т.к. длина участка 2-3 несравнимо мала с длиной 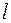. Пусть в результате расчетов определено: 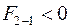; ; 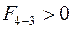и .

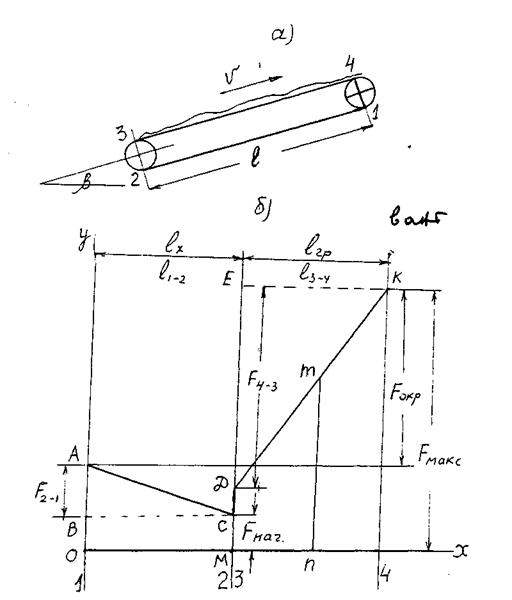
Рис. 5.5. Диаграмма натяжений гибкого тягового органа

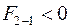На линии 1 выбирается произвольно точка А и от нее вниз, в выбранном масштабе откладывается сила тяги (вниз, потому, что ). Полученная точка В сносится на линию 2 (точка С). Величина силы 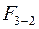откладывается вверх на линии 3 (точка Д), а от нее вверх откладывается сила 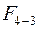(точка Е) и сносится на линию 4 (точка К). Прямыми линиями (т.к. сила тяги линейно зависит от длины) соединяются точки А, С, Д и К. Полученная таким образом диаграмма показывает пока только картину распределения натяжений: от точки А к С натяжение уменьшается, а далее – увеличивается. Величину же натяжения в любой точке (в любом сечении контура) можно узнать только после нахождения положения оси абсцисс на диаграмме. Ясно, что ось не может быть выше точки С, т.к. в противном случае значения сил ниже оси означали бы сжатие. Т.о. положение оси абсцисс, совпадающее с линией ВС, самое высшее, которое может быть (теоретически) во время работы транспортного средства. В этом случае тяговый орган предварительно не натянут и все натяжения в нем создаются в результате преодоления сил сопротивления (приложения сил тяги). На практике же, в зависимости от разных (дополнительных) требований тяговый орган необходимо предварительно натягивать (создавать первоначальное натяжение). Чем больше это натяжение 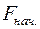, тем ниже положение оси абсцисс. Пусть 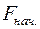известно (например по условиям минимального натяжения цепи на скребковом конвейере для обеспечения ее хода на звездочке или по условиям минимального натяжения ленты ленточного конвейера по условиям ограничения провеса ее между роликоопорами). Величина 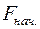в данном случае откладывается вниз от самой нижней точки диаграммы (точка С) и через полученную точку М проводится ось . В иных случаях величина начального натяжения может откладываться и от других точек. Эта положительная величина откладывается вниз потому, что от оси вверх будут считаться положительные натяжения.

Построение диаграммы закончено. Любая ордината – величина натяжения тягового органа в выбранном масштабе сил. Например, натяжение в точке 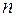, расположенной посредине груженной ветви, равно отрезку , умноженному на масштаб. Диаграмма показывает сечение с максимальным натяжением в точке К, величину тягового усилия приводного блока и др.

Из диаграммы видно, какая часть натяжения в каждом сечении создается за счет начального натяжения, а какая – за счет силы тяги.

Диаграмму натяжений можно также построить непосредственно на схеме контура тягового органа, что менее удобно.

Рекомендуемая литература:

1. Біліченко М.Я. Основи теорії та розрахунки транспортних засобів механізації переміщення вантажів шахт. Навчальний посібник - Дніпропетровськ: НГУ, 2002. –102с. (стр.)

2. Транспорт на горных предприятиях / Под ред.. проф, Б.Л. Кузнецова. М.: Недра, 1976, - 552 с. (стр.)

3. Основные положения по проектированию подземного транспорта для новых и действующих угольных шахт. - М,: ИГД им. А.А. Скочинского, 1986, - 355 с.

4. Шахтный транспорт шахт и рудников: Справочник / Под ред. Г.Я. Пейсаховича, И.Л. Ремизова. - М.: Недра, 1985. - 565 с.

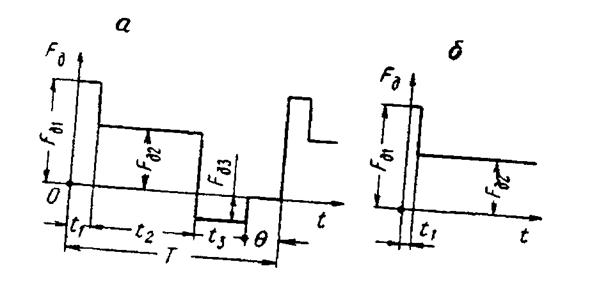
Рис. 5.4. Нагрузочные диаграммы двигателей

Рис. 5.5. Диаграмма натяжений гибкого тягового органа

Дата добавления: 2014-01-06