Преобразование уравнения к итерационному виду

Уравнение F (x) = 0 преобразуется к виду, пригодному для итерационного процесса, следующим преобразованием

,

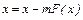где m - отличная от нуля константа.

В этом случае

. (2.15)

Функция f (x) должна удовлетворять условиям теоремы 2.2. Дифференцируя (2.15), получим

. (2.16)

Для выполнения условия 3 теоремы 2.2, достаточно подобрать m, так чтобы для всех х Î

. (2.17)

Пример 2.2. Решение уравнения методом простой итерации в пакете MАTLAB

1. Создание файла Func.m, содержащего описание функции

% листинг файла Func.m

function z=Func(x)

z=x.^4-11*x.^3+x.^2+x+0.1;

2. Создание файла Func1.m, содержащего описание функции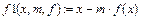

% листинг файла Func1.m

function z=Func1(x,m,f)

z=x-m*feval(f,x);

3. Создание файла Func2, содержащего описание функции f 2 (2.16)

% листинг файла Func2.m

function z=Func2(x,m,f)

dx=10^-7;

x1=x+dx;

tmp1=x-m*feval(f,x);

tmp2=x1-m*feval(f,x1);

z=abs((tmp2-tmp1)/dx);

4. Построение графиков функций f 1, f 2 (рис. 2.6)

>> dx=10^-3;

>> x1=-0.1;x2=0.8;

>> x=x1:dx:x2;

>> m=-0.05;

>> plot(x,Func1(x,m,'Func'));

>> hold on

>> plot(x,Func2(x,m,'Func'),'--');

>> grid on

Рис. 2.6

(Из рис. 2.6 видно, что условия о достаточном условии сходимости итерационного процесса выполняются на интервале [0.21;0.8].)

5. Создание файла My_Iter.m, описание функции, возвращающей значение производной на каждом шаге итерационного процесса

% листинг функции My_Iter.m

function z=My_Iter(f,x0,eps,q,m)

x(1)=x0;

i=1;

while abs(x(i)-Func1(x(i),m,f))>q/(1-q)*eps

x(i+1)=Func1(x(i),m,f);

i=i+1;

end;

z=x;

6. Задание параметров итерационного процесса

>> q=0.01;

>> eps=10^-5;

7. Вычисление значений корня уравнения на каждом шаге итерационного процесса

>> z=My_Iter('Func',x0,eps,q,m)

8. Визуализация итерационного процесса (рис. 2.8)

>> plot(z,'-o');

Рис. 2.9

9. Вывод точного значения корня

>> Ni=length(z);

>> z(Ni)

ans =

0.3942

10. Вывод значения функции

>> Func(z(Ni))

ans =

-1.8185e-006

Для вычисление нулей функций, зависящих от одной перемененной, в пакете MATLAB предусмотрена специальная функции fzero(), реализующая в зависимости от вида функции методы половинного деления, секущих или обратной квадратичной интерполяции. Обращение к данной функции имеет следующий вид:

x = fzero(fun,x0)

x = fzero(fun,x0,options)

x = fzero(fun,x0,options,P1,P2,...)

[x,fval] = fzero(...)

[x,fval,exitflag] = fzero(...)

[x,fval,exitflag,output] = fzero(...)

Здесь

fun - строковая переменная, содержащая имя файла;

x0 - начальное приближение или интервал поиска решения;

options - параметры, задающие точность и способ представления результатов вычислений;

P1, P2, … - дополнительные аргументы, передаваемые в функцию fun (F=feval(FUN,X,P1,P2,...));

fval - переменная, в которую функция fzero() возвращает значение корня уравнения f (x)=0;

exitflag - переменная, знак которой свидетельствует о наличии корня на данном интервале (exitflag =1 - корень существует);

output - переменная, в которую функция fzero() возвращает название метода, использованного для нахождения корня уравнения.

Пример 2.3. Решение уравнения с использованием функции fzero().

>> x=fzero('Func',0.8)

x =

Дата добавления: 2014-01-06