Выражения

50.0000

39.9999

29.9995

20.0003

10.0013

0.8947

1.6564

1.4325

0.0972

Else

C1(i,j)=-C(i,j)/C(i,i);

end;

end;

end;

% решение системы линейных уравнений методом Зейделя

R1=d1;

while Flag==0

for i=1:N

v=C1(i,1:N); % выделение i -oй строки матрицы

a=dot(v',d1); % вычисление скалярного произведения

d1(i)=a+D1(i);

end;

R2=d1;

s=max(abs(R2-R1));

if s<eps

z1=d1;

z2=s;

return

end;

R1=R2;

end;

2. Задать матрицу коэффициентов при неизвестных исходной системы линейных уравнений и столбец свободных членов

>> A=[1,2,3,4,5;10,9,8,7,6;5,9,11,12,13;20,1,3,17,14;12,10,4,16,15]

>> b=[10,20,30,40,50];

3. Вычислить решение системы линейных уравнений, используя функцию Zeidel()

>> Zeidel1(A,b,10^-6)

ans =

-1.3533

4. Проверить полученное решение

>> A*ans

ans =

3.6. Решение систем линейных уравнений средствами пакета MATLAB

Для решения систем линейных уравнений и связанных с ними матричных операций применяются операторы: сложения (+), вычитания (-), умножения (*), деления справа (/), деления слева (\), возведения в степень (^), транспонирования (¢), действие которых определяется правилами линейной алгебры.

Пусть задана система n линейных алгебраических уравнений с n неизвестными:

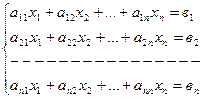. (3.61)

Система уравнений (1) в матричной форме представляется следующим образом:

АХ = В, (3.62)

где А – квадратная матрица коэффициентов, размером n ´ n строк и столбцов;

Х – вектор-столбец неизвестных;

В – вектор-столбец правых частей.

Систему уравнений (2) можно решить различными методами. Один из наиболее простых и эффективных методов является метод исключения Гаусса и его модификации. Алгоритм метода основан на приведении матрицы А к треугольному виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти процедуры можно выполнять над невырожденными матрицами, в противном случае метод Гаусса неприменим.

Недостатком метода является накапливание погрешностей в процессе округления, поэтому метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших (n £ 100) систем уравнений с плотно заполненной матрицей и не близким к нулю определителем. Если матрица А сильно разрежена, а ее определитель не близок к нулю, то метод Гаусса не пригоден для решения больших систем уравнений.

В MATLAB имеется обширный арсенал методов решения систем уравнений (2). Для этого применяются следующие операторы

/	- правое деление;
\	- левое деление;
Ù - 1	- возведение в степень –1;
inv(A)	- обращение матрицы А.

Х=В’/A’

Х=В’* (А^ - 1)’

Х=В’* inv(A’)

Х=A\В

дают решения ряда систем линейных уравнений АХ = В, где А – матрица размером m ´ n, В – матрица размером m ´ к. Более сложные случаи решения систем уравнений (2) с плохо обусловленной матрицей А требуют применения специальных методов решения.

Для решения системы линейных уравнений вида

Ax = b,

где A - матрица коэффициентов при неизвестных, x - вектор-столбец неизвестных, b - вектор-столбец свободных членов, в пакете MATLAB достаточно выполнить следующую команду:

>> A^-1*b

Пример 1.

Решить систему 4-х линейных уравнений:

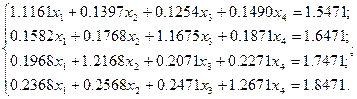
Протокол программы (в скрипт-файле)

a= [1.1161 0.1397 0.1254 0.1490;

Дата добавления: 2014-01-06