Нахождение приближающей функции в виде линейной функции и квадратичного трехчлена

Сумма квадратов отклонений

Значения разностей

(7.9)

называют отклонениями измеренных значений от вычисленных по формуле (7.5).

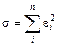(7.10)

в соответствие с принципом наименьших квадратов для заданного вида приближающей функции должна быть наименьшей.

Из двух разных приближений одной и той же табличной функции лучшим считается то, для которого (7.10) имеет наименьшее значение.

Ищем приближающую функцию в виде:

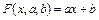. (7.11)

Находим частные производные

. (7.12)

Составляем систему вида (7.8)

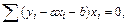
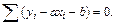
(Здесь и далее сумма ведется по переменной .)

Далее имеем

,

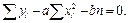(7.13)

Разделив каждое уравнение (7.13) на n, получаем

,

.

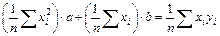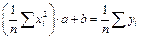Введем обозначения

.

Тогда последняя система будет иметь вид

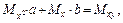
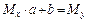
или в матричной форме

.

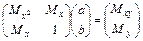Откуда

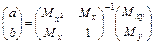. (7.14)

Вычислив значения параметров a, b в соответствие с (7.14), получаем конкретные значения и, следовательно, конкретный вид линейной функции (7.11).

В случае нахождения приближающей функции в форме квадратного трехчлена имеем:

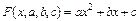. (7.15)

Находим частные производные:

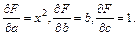
Составляем систему вида (7.8)

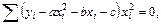
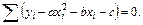
Далее имеем

,

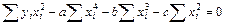Разделив каждое уравнение на n и перенеся члены, не содержащие неизвестные параметры в правую часть получаем:

,

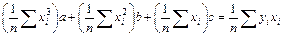, (7.16)

.

Решив систему (7.16) относительно неизвестных a, b, c, находим значения параметров приближающей функции.

Рис. 7.2

Для нахождения решения задачи о нахождении линейного и квадратичного трехчленов в пакете MATLAB необходимо выполнить следующую последовательность команд:

% задание исходных данных

>> N=10;

>> i=1:N;

>> Xmin=0;

>> Xmax=10;

>> x(i)=Xmin+(Xmax-Xmin)/(N-1)*(i-1);

>> y(i)=0.2*x(i); % точные значения функции

% задание шума с равномерным законом распределения на

% отрезке [b,a]

>> a=0.2

>> b=-0.1;

>> Yrnd=b+(a-b)*rand(N,1);

>> y1=y+Yrnd'; % создание зашумленных данных

>> plot(x,y,x,y1,'o'); % визуализация точной и зашумленной

% последовательностей (рис. 7.2)

% вычисление элементов матрицы M в (7.14)

>> tmp=x(i).^2;

>> M(1,1)=1/N*sum(tmp);

>> M(1,2)=1/N*sum(x);

>> M(2,1)=M(1,2);

>> M(2,2)=1;

% вычисление элементов вектора d

>> d(1,1)=1/N*dot(x,y1);

>> d(2,1)=1/N*sum(y1);

% решение системы линейных уравнений (7.14)

>> Coeff=A^-1*d;

Coeff =

Дата добавления: 2014-01-06