Аппроксимация функцией произвольного вида

0.5126

3.0521

1.0000 1.0000 0.5000

0.6400 0.8000 0.5556

0.3600 0.6000 0.6250

0.1600 0.4000 0.7143

0.0400 0.2000 0.8333

0 0 1.0000

2.0000

1.0000

0.1200

0.8000

0.2200

0.4300

1.0000

0.8000

0.6000

0.4000

0.2000

0.0004

0.1904

0.1049

1.0000 10.0000 100.0000

1.0000 8.8889 79.0123

1.0000 7.7778 60.4938

1.0000 6.6667 44.4444

1.0000 5.5556 30.8642

1.0000 4.4444 19.7531

1.0000 3.3333 11.1111

1.0000 2.2222 4.9383

1.0000 1.1111 1.2346

1.0000 0 0

0.0687

Dot(tmp,tmp)

0.1049

0.1904

0.0004

0.0685

0.0993

0.1941

>> F=inline('a*x+b','a','b','x'); % задание аппроксимирующей

% функции

>> tmp1(i)=feval(F,Coeff(1,1),Coeff(2,1),x(i)); % вычисление

% значений

% аппроксимирующей

% функции

% вычисление суммы квадратов отклонений

% при линейной аппроксимации

>> tmp=tmp1-y1;

>> dot(tmp,tmp)

ans =

% аппроксимация исходных данных полиномом второй степени

% задание матрицы системы линейных уравнений в (7.16)

>> A(1,1)=1/N*sum(x.^4);

>> A(1,2)=1/N*sum(x.^3);

>> A(1,3)=1/N*sum(x.^2);

>> A(2,1)=A(1,2);

>> A(2,2)=A(1,3);

>> A(2,3)=1/N*sum(x);

>> A(3,1)=A(2,2);

>> A(3,2)=A(2,3);

>> A(3,3)=1;

% задание вектора столбца свободных членов

>> d(1,1)=1/N*dot(x.^2,y1);

>> d(2,1)=1/N*dot(x,y1);

>> d(3,1)=1/N*sum(y1);

% решение системы линейных уравнений (7.16)

>> Coeff=A^-1*d

Coeff =

>> F=inline('a*x.^2+b*x+c','a','b','c','x'); % задание

% аппроксимирующей

% функции

% вычисление суммы квадратов отклонений при квадратичной

% интерполяции

>> tmp2(i)=feval(F,Coeff(1,1),Coeff(2,1),Coeff(3,1),x(i));

>> tmp=tmp2-y1;

ans =

Можно найти решение рассмотренной выше задачи регрессии в пакете MATLAB можно другим способом. Для следует использовать тот факт, что коэффициенты искомой функции, минимизирующей сумму квадратов отклонений, являются решением переопределенной системы уравнений. Для случая интерполяции полиномом второй степени данных, приведенных выше, система уравнений имеет вид:

.

Решение данной системы уравнений, удовлетворяющее методу наименьших квадратов, находится с помощью оператора \:

Coeff = A\y1,

где

,

.

Рис. 7.2

Таким образом, альтернативный подход к нахождению коэффициентов аппроксимирующего полинома реализуются выполнением следующей последовательности команд:

>> B=[ones(size(x')) x' x'.^2]

B =

>> Coeff=B\y1

ans =

Для решения системы линейных уравнений метода наименьших квадратов при использовании аппроксимации линейной комбинацией известных функций в пакете MATLAB можно использовать метод, описанный в предыдущем разделе. Ниже представлена последовательность команд, позволяющая найти коэффициенты аппроксимирующей функции вида .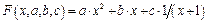

% Задание исходных данных

>> vx=[0;0.2;0.4;0.6;0.8;1]

vx =

>> vy=[0.43;0.22;0.8;0.12;1;2]

vy =

% задание матрицы переопределенной системы уравнений

>> D=[vx.^2 vx 1./(vx+1)]

>> D

D =

>> Coeff=D\vy

Coeff =

-1.4391

% визуализация исходных данных и аппроксимирующей функции

>> i=1:length(vx);

>> j=1:length(X);

>> X=vx(1):0.01:vx(6);

>> Y=[ones(size(X')) X' X'.^2]*Coeff; % вычисление значений

% аппроксимирующей

% функции

>> plot(vx(i),vy(i),'o',X(j),Y(j)) % (рис. 7.3)

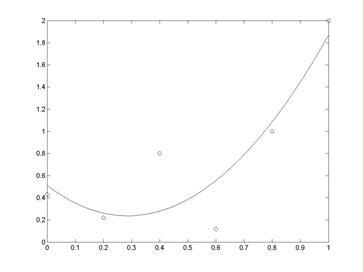
Рис. 7.3

Для решения задачи обобщенной нелинейной регрессии в пакете MATLAB имеется функция lsqnonlin(), возвращающая решение задачи нахождения точки минимума функции f (x)

,

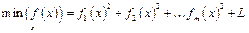где в общем случае f (x) -вектор-функция, x - вектор-столбец искомых переменных, L - некоторая константа.

Синтаксис функции lsqnonlin():

x = lsqnonlin(fun,x0)

x = lsqnonlin(fun,x0,lb,ub)

x = lsqnonlin(fun,x0,lb,ub,options)

x = lsqnonlin(fun,x0,eb,ub,options,P1,P2,...)

[x,resnorm] = lsqnonlin(...)

[x,resnorm,residual] = lsqnonlin(...)

[x,resnorm,residual,exitflag] = lsqnonlin(...)

[x,resnorm,residual,exitflag,output] = lsqnonlin(...)

[x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...)

[x,resnorm,residual,exitflag,output,lambda,jacobian] =

lsqnonlin(...)

аналогичен синтаксису функции fsolve(), подробно обсуждавшемся нами в лекции № 4. Поэтому далее мы ограничимся только примером, демонстрирующим использование данной функции для нахождения параметров функции .

Для решения данной задачи в пакете MATLAB необходимо выполнить следующую последовательность действий:

1. Создать файл F77.m, содержащий описание функции, возвращающей значения вектор-функции f (x)

% листинг файла F77.m

function z=F77(Coeff,vx,vy)

k=1:length(vx);

z=vy-exp(Coeff(1)+Coeff(2)*vx+Coeff(3)*vx.^2);

2. Выполнить следующую последовательность команд

% задание исходных данных

>> vx=[0.3;0.4;1;1.4;2;4]

vx =

Дата добавления: 2014-01-06