Метод Эйлера

В основе метода Эйлера лежит идея графического построения решения ДУ (рис. 9.1).

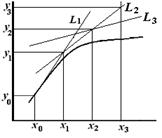
Рис. 9.1

Пусть дано уравнение (9.2) с начальным условием . Выбрав достаточно малый шаг h, построим, начиная с точки 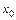, систему равноотстоящих точек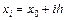 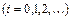. Вместо искомой интегральной кривой на отрезке 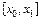рассмотрим отрезок касательной к ней в точке , уравнение которой .

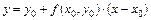При 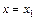из уравнения касательной получаем 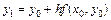. Следовательно, приращение функции на первом шаге равно .

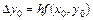Проведя аналогично касательную к интегральной кривой в точке в точке 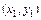, получим:

,

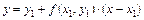что при 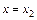дает , т.е. получается из добавлением приращения .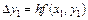

Таким образом, вычисление таблицы значений функции, являющейся решением ДУ (2.8), состоит в последовательном применении пары формул:

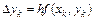, (9.24)

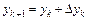. (9.25)

Метод Эйлера, как, видно из рисунка, имеет погрешность. Определим локальную погрешность, присутствующую на каждом шаге, которая определяется разностью между точным значением функции и соответствующим значением касательной. Для первого шага:

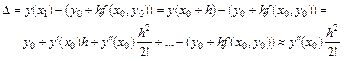(9.26)

Из (9.26) видно, что локальная погрешность пропорциональна 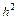. Суммарная погрешность 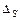после N шагов пропорциональна 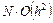, поскольку , то 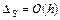, т.е. метод Эйлера - метод первого порядка точности по h.

Известны различные уточнения метода Эйлера. Модификации данных методов направлены на уточнение направления перехода из точки в точку Например, в методе Эйлера-Коши используют следующий порядок вычислений:

,

. (9.27)

Геометрически это означает, что определяется направление интегральной кривой в исходной точке и во вспомогательной точке , а в качестве окончательного берется среднее значение этих направлений.

Пример 9.1. Найти решение задачи Коши дифференциального уравнения

, ,

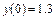методами Эйлера и методом Эйлера-Коши.

1. Нахождение численного решения ДУ методом Эйлера.

Для нахождения решения данного ДУ необходимо создать файл Euler.m, содержащий описание функции, возвращающей решение дифференциального уравнения методом Эйлера.

% листинг файла euler_g9.m

function [X,Y]=Euler_g9(y0,x0,x1,N)

dx=(x1-x0)/N;

x(1)=x0;

y(1)=y0;

for i=1:N

x(i+1)=x(1)+dx*i;

y(i+1)=y(i)+dx*F9(x(i));

end;

X=x;

Y=y;

function z=F9(x)

z=x.^2;

Далее необходимо выполнить следующую последовательность команд:

>> x0=0; % левая граница отрезка интегрирования

>> x1=5; % правая граница отрезка интегрирования

>> y0=1.3; % начальное условие

>> N=50; % число узлов разбиения отрезка интегрирования

>> [X Y]=Euler_g9(y0,x0,x1,N); % нахождение численного решения

% задачи Коши

>> i=1:length(X);

>> Z(i)=y0+1/3*X(i).^3; % вычисление значений точного решения

>> plot(X,Z,X,Y,':') % визуализация точного и численного решений

% (рис. 9.2)

>> plot(X,abs(Z-Y)) % визуализация разности между численным и

% точным решениями ДУ (рис. 9.3)

2. Нахождение численного решения ДУ методом Эйлера-Коши.

Для нахождения решения данного ДУ необходимо создать файл EulerKoshi, содержащий описание функции, возвращающей решение дифференциального уравнения методом Эйлера-Коши.

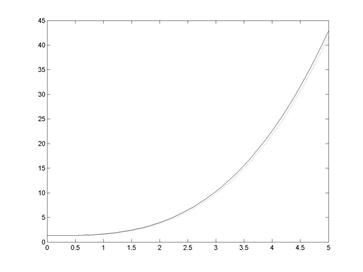
Рис. 9.2

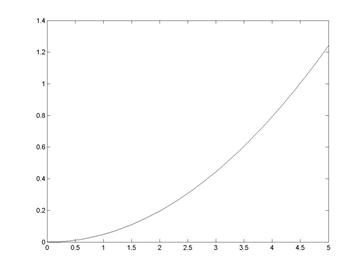
Рис. 9.3

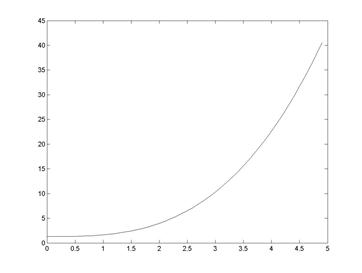
Рис. 9.4

% листинг файла EulerKoshi.m

function [X,Y]=EulerKoshi(y0,x0,x1,N)

dx=(x1-x0)/N;

x(1)=x0;

y(1)=y0;

for i=2:N

x(i)=x(1)+dx*(i-1);

Z=y(i-1)+dx*F9(x(i-1),y(i-1));

y(i)=y(i-1)+(F9(x(i-1),y(i-1))+F9(x(i),Z))*dx/2;

end;

X=x;

Y=y;

function z=F9(x,y)

z=x.^2;

Далее необходимо выполнить следующую последовательность команд:

>> x0=0; % левая граница отрезка интегрирования

>> x1=5; % правая граница отрезка интегрирования

>> y0=1.3; % начальное условие

>> N=50; % число узлов разбиения отрезка интегрирования

>> [X Y]=EulerKoshi(y0,x0,x1,N); % нахождение численного

% решения задачи Коши

>> i=1:length(X);

>> Z(i)=y0+1/3*X(i).^3; % вычисление значений точного решения

>> plot(X,Z,X,Y,':') % визуализация точного и численного решений

% (рис. 9.4)

>> plot(X,abs(Z-Y)) % визуализация разности между численным и

% точным решениями ДУ (9.5)

Рис. 9.5

Из сравнения рис. 9.3, 9.5 видно, что погрешность, как и ожидалось уменьшилась в 10² раз (h = 0.1).

Дата добавления: 2014-01-06