Метод Рунге-Кутта

Метод Эйлера и метод Эйлера относятся к семейству методов Рунге-Кутта. Для построения данных методов можно использовать следующий общий подход. Фиксируем некоторые числа:

.

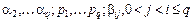Последовательно вычисляем:

,

,

…

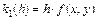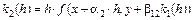и полагаем:

. (9.28)

Рассмотрим вопрос о выборе параметров . Обозначим

.

Будем предполагать, что

,

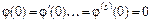а 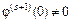для некоторой функции .

По формуле Тэйлора справедливо равенство

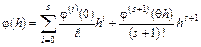, (9.29)

где .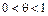

При будем иметь:

,

.

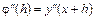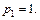Ясно, что равенство выполняется для любых функций лишь при условии, что При данном значении 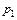из формулы (9.28) получаются формулы (9.24), (9.25) метода Эйлера. Погрешность данного метода на шаге согласно (9.29) равна

.

Рассмотрим случай 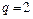, тогда

,

где .

Согласно исходному дифференциальному уравнению

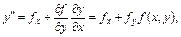
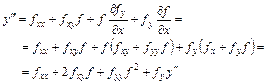(9.30)

Вычисляя производные функции 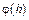и, подставляя в выражения для 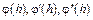значение , получаем

,

. (9.31)

Требование

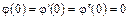
будет выполняться для всех только в том случае, если одновременно справедливы следующие три равенства относительно четырех параметров:

,

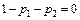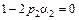, (9.32)

Задавая произвольно значения одного из параметров и определяя значения остальных из системы (9.32), можно получать различные методы Рунге-Кутта с порядком погрешности . Например, при 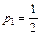из (9.32) получаем: , .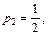

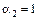Для выбранных значений параметров (9.28) приобретает следующий вид:

.

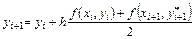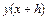(Здесь записано вместо , - вместо 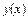, а через обозначено выражение .)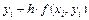

Таким образом, для рассматриваемого случая приходим к расчетным формулам (9.27) метода Эйлера-Коши. Из (9.29) следует, что главная часть погрешности на шаге есть

,

т.е. погрешность пропорциональна третьей степени шага.

На практике наиболее часто используют метод Рунге-Кутта с 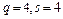. Данный метод реализуются в соответствие со следующими расчетными формулами:

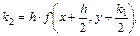
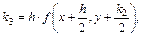(9.33)

.

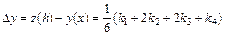Погрешность рассматриваемого метода Рунге-Кутта на шаге пропорциональна пятой степени шага.

Геометрический смысл использования метода Рунге-Кутта с расчетными формулами состоит в следующем. Из точки сдвигаются в направлении, определяемом углом , для которого 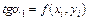. На этом направлении выбирается точка с координатами 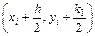. Затем из точки сдвигаются в направлении, определяемым углом , для которого , и на этом направлении выбирается точка с координатами . Наконец из точки , сдвигаются в направлении, определяемом углом 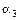, для которого и на этом направлении выбирается точка с координатами 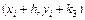. Этим задается еще одно направление, определяемое углом 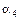, для которого . Четыре, полученные направления усредняются в соответствие с (9.33). На этом окончательном направлении и выбирается очередная точка .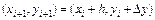

Пример 9.2. Найти решение задачи Коши дифференциального уравнения

,

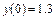
методом Рунге-Кутта четвертого порядка.

Для нахождения решения данного ДУ необходимо создать файл RungeKutt4.m, содержащий описание функции, возвращающей решение дифференциального уравнения методом Рунге-Кутта четвертого порядка.

% листинг файла RungeKutt4.m

function [X,Y]=RungeKutt4(y0,x0,x1,N)

dx=(x1-x0)/N;

x(1)=x0;

y(1)=y0;

for i=2:N

x(i)=x(1)+dx*(i-1);

k1=dx*F9(x(i-1),y(i-1));

k2=dx*F9(x(i-1)+dx/2,y(i-1)+k1/2);

k3=dx*F9(x(i-1)+dx/2,y(i-1)+k2/2);

k4=dx*F9(x(i-1)+dx,y(i-1)+k3);

y(i)=y(i-1)+1/6*(k1+2*k2+2*k3+k4);

end;

X=x;

Y=y;

function z=F9(x,y)

z=x.^2;

Далее необходимо выполнить следующую последовательность команд:

>> x0=0; % левая граница отрезка интегрирования

>> x1=5; % правая граница отрезка интегрирования

>> y0=1.3; % начальное условие

>> N=50; % число узлов разбиения отрезка интегрирования

>> [X Y]=RungeKutt4(y0,x0,x1,N); % нахождение численного

% решения задачи Коши

>> i=1:length(X);

>> Z(i)=y0+1/3*X(i).^3; % вычисление значений точного решения

>> plot(X,Z,X,Y,':') % визуализация точного и численного решений

% (рис. 9.6)

>> plot(X,abs(Z-Y)) % визуализация разности между численным и

% точным решениями ДУ (9.7)

Дата добавления: 2014-01-06