Средства пакета MATLAB для решения обыкновенных дифференциальных уравнений

Метод Рунге-Кутта 4-го порядка решение задачи Коши для ДУ в пакете MATLAB реализован в виде функции ode45. Данный метод рекомендуется использовать при первой попытке нахождения численного решения задачи.

Помимо данной функции в пакете MATLAB реализованы и другие

Рис. 9.6

Рис. 9.7

методы решения дифференциальных уравнений и систем ДУ:

ode23 - функция реализует одношаговые явные методы Рунге-Кутта (2 и 3) порядков. Функция используется при решении нежестких систем ДУ обеспечивает удовлетворительную точность при меньших нежели функция ode45 временных затратах.

ode113 -функция реализует многошаговый метод Адамса-Башворта-Мултона переменного порядка. Функция используется при необходимости обеспечить высокую точность численного решения.

ode15s -функция реализуетмногошаговый метод переменного порядка (от 1 до 5 по умолчанию), основанный на формулах численного дифференцирования. Данный метод следует использовать в том случае, если не удается найти численное решение с помощью функции ode45.

ode23s - функция реализуетодношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Данной метод обеспечивает более высокую скорость вычислений по сравнению с другими методами при сравнении с другими методами при относительно более низкой точности вычислений.

ode23t - функция реализует метод трапеций с интерполяцией. Данный метод используют при решении уравнений, описывающих колебательные системы с почти гармоническим выходным сигналом.

ode23tb - функция реализует неявный метод Рунге-Кутта в начале интервала интегрирования и далее метод, использующий формулы обратного дифференцирования 2-го порядка. Данный метод обладает большей скорость нежели метод ode15s при, соответственно, меньшей точности.

Все перечисленные выше функции, называемые в документации пакета Solver (решатель), могут решать системы ДУ явного вида 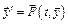. Кроме того решатели ode15s, ode23s, ode23t и ode23tb системы дифференциальных уравнений неявного вида 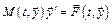, а также все решатели, кроме ode23s, могут находить решения уравнения вида .

Пример 9.3. Решение задачи Коши для дифференциального уравнения

,

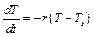T (0)=80.

где T_s, r - заданные постоянные, имеющие физический смысл температуры окружающей среды и коэффициента остывания, соответственно,

Для решения дифференциального уравнения (2.1) сначала создаем m-файл, содержащий определение функции, стоящей в правой части уравнения (2.1):

function Z=Tempr(t,T)

% определение функции, стоящей в правой части уравнения (2.1)

Дата добавления: 2014-01-06