Активационные функции

1. Жесткая ступенька: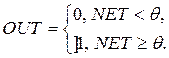

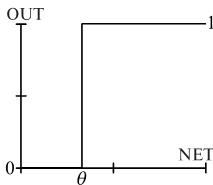
Рис. Жесткая ступенька.

Здесь θ – пороговый уровень нейрона. Данная функция используется в классическом искусственном нейроне. Нейроны с такой нелинейностью требуют малых вычислительных затрат. Данная функция чрезмерно упрощена и не позволяет моделировать схемы с непрерывными сигналами. Отсутствие первой производной затрудняет применение градиентных методов для обучения таких нейронов.

2. Логистическая функция (сигмоида):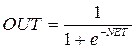

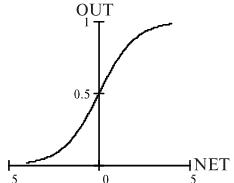
Рис. Логистическая функция.

Эта функция часто применяется для сетей с непрерывными сигналами.

Она симметрична относительно точки с координатами NET = 0, OUT = 0,5, что делает равноправными значения OUT = 0 и OUT = 1. Тем не менее диапазон выходных значений от 0 до 1 несимметричен, что замедляет обучение соответствующей нейронной сети. Данная функция является сжимающей, т.к для малых значений NET коэффициент передачи K = OUT/NET велик, для больших значений он снижается. Поэтому диапазон сигналов, с которыми нейрон работает без насыщения, оказывается широким. Производная непрерывна и легко выражается через саму функцию, что ускоряет обучение нейрона.

3. Гиперболический тангенс: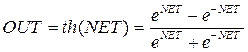

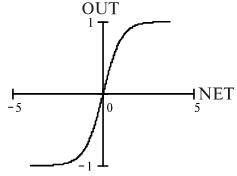
Рис. Гиперболический тангенс

Также часто применяется для сетей с непрерывными сигналами. Фунция симметрична относительно точки (0, 0), что является преимуществом по сравнению с сигмоидой. Производная также непрерывна и легко выражается через саму функцию.

4. Пологая ступенька: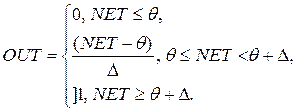

Легко рассчитывается, но имеет разрывную производную в точках NET = θ, NET = θ + Δ, что усложняет алгоритм обучения.

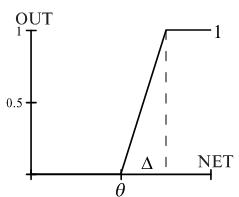
Рис. Пологая ступенька.

5. Гауссова кривая: .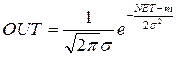

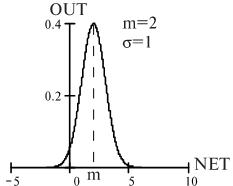
Рис. Гауссова кривая.

Применяется в случаях, когда реакция нейрона должна быть максимальной для некоторого определенного значения NET.

Выбор функции активации определяется следующими факторами:

1. Спецификой задачи.

2. Удобством реализации на ЭВМ, в виде электрической схемы или другим способом.

3. Алгоритмом обучения: некоторые алгоритмы накладывают ограничения на вид функции акти­вации, что необходимо учитывать.

Чаше всего вид нелинейности не оказывает принципиального влияния на решение задачи. Одна­ко удачный выбор может сократить время обучения в несколько раз.

Дата добавления: 2014-01-06