Однослойные искусственные нейронные сети

Ограничения модели нейрона

1. Вычисления выхода нейрона предполагаются мгновенными, не вносящими задержки. Непо­средственно моделировать динамические системы, имеющие "внутреннее состояние", с помо­щью таких нейронов нельзя.

2. В модели отсутствуют нервные импульсы. Нет модуляции уровня сигнала плотностью импуль­сов, как в нервной системе. Не появляются эффекты синхронизации, когда скопления нейро­нов обрабатывают информацию синхронно, под управлением периодических волн возбужде­ния-торможения.

3. Нет четких алгоритмов для выбора функции активации.

4. Нет механизмов, регулирующих работу сети в целом (пример - гормональная регуляция активности в биологических нервных сетях).

5. Чрезмерная формализация понятий: "порог", "весовые коэффициенты". В реальных нейронах нет числового порога, он динамически меняется в зависимости от активности нейрона и обще­го состояния сети. Весовые коэффициенты синапсов тоже не постоянны. "Живые" синапсы обладают пластичностью и стабильностью: весовые коэффициенты настраиваются в зависимо­сти от сигналов, проходящих через синапс.

6. Существует большое разнообразие биологических синапсов. Они встречаются в различных частях клетки и выполняют различные функции. Тормозные и возбуждающие синапсы реали­зуются в данной модели в виде весовых коэффициентов противоположного знака, по разнооб­разие синапсов этим не ограничивается. Дендро-дендритные. аксо-аксональные синапсы не
реализуются в модели ФН.

7. В модели не прослеживается различие между градуальными потенциалами и нервными им­пульсами. Любой сигнал представляется в виде одного числа.

Итак, модель формального нейрона не является биоподобпой и скорее похожа на математичес­кую абстракцию, чем на живой нейрон. Тем не менее с помощью таких нейронов решается большое многообразие задач.

Хотя один нейрон и способен решать простейшие задачи, сила нейронных вычислений проистекает от соединений нейронов в сетях.

Существуют два подхода к созданию искусственных нейронных сетей.

1. Биологический подход, где при моделировании важно полное биоподобие, и необходимо детально изучать работу биологического нейрона.

2. Информационный подход при котором безразлично, какие механизмы лежат в основе работы искусственных нейронных сетей, важно лишь, чтобы при решении задач информационные процессы в НС были подобны биологическим.

Простейшая сеть состоит из группы нейронов, образующих слой, как показано в правой части рис. 1.5.

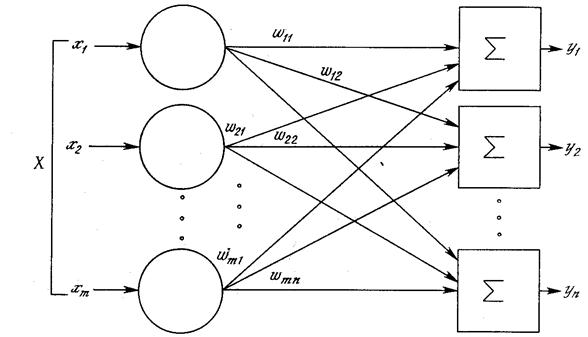
Рис. 1.5. Однослойная нейронная сеть

Отметим, что вершины-круги слева служат лишь для распределения входных сигналов. Они не выполняют каких- либо вычислений, и поэтому не будут считаться слоем. По этой причине они обозначены кругами, чтобы отличать их от вычисляющих нейронов, обозначенных квадратами. Каждый элемент из множества входов Х отдельным весом соединен с каждым искусственным нейроном. А каждый нейрон выдает взвешенную сумму входов в сеть. В искусственных и биологических сетях многие соединения могут отсутствовать, все соединения показаны в целях общности. Могут иметь место также соединения между выходами и входами элементов в слое.

Удобно считать веса элементами матрицы W. Матрица имеет т строк и п столбцов, где m – число входов, а n – число нейронов. Например, w _2,3 – это вес, связывающий третий вход со вторым нейроном. Таким образом, вычисление выходного вектора N, компонентами которого являются выходы OUT нейронов, сводится к матричному умножению N = XW, где N и Х – векторы-строки.

Дата добавления: 2014-01-06