Однослойный персептрон

Персептронная представляемость

Выбор количества нейронов и слоев

Не существует строго определенной процедуры для выбора количества нейронов и количества слоев в сети. Чем больше количество нейронов и слоев, тем шире возможности сети, тем медленнее она обучается и работает и тем более нелинейной может быть зависимость вход-выход.

Количество нейронов и слоев связано:

1) со сложностью задачи;

2) с количеством данных для обучения;

3) с требуемым количеством входов и выходов сети;

4) с имеющимися ресурсами: памятью и быстродействием машины, на которой моделируется сеть;

Были попытки записать эмпирические формулы для числа слоев и нейронов, но применимость формул оказалась очень ограниченной.

Если в сети слишком мало нейронов или слоев:

1) сеть не обучится и ошибка при работе сети останется большой;

2) на выходе сети не будут передаваться резкие колебания аппроксимируемой функции y (x).

Превышение требуемого количества нейронов тоже мешает работе сети.

Если нейронов или слоев слишком много:

1) быстродействие будет низким, а памяти потребуется много — на фон-неймановских ЭВМ;

2) сеть переобучится: выходной вектор будет передавать незначительные и несущественные детали в изучаемой зависимости y (x), например, шум или ошибочные данные;

3) зависимость выхода от входа окажется резко нелинейной: выходной вектор будет существенно и непредсказуемо меняться при малом изменении входного вектора x;

4) сеть будет неспособна к обобщению: в области, где нет или мало известных точек функции y (x) выходной вектор будет случаен и непредсказуем, не будет адекватен решаемой задаче.

Сложность задач, решаемых персептроном, существенно зависит от количества слоев. Рассмотрим эти различия.

Круг проблем, которые под силу однослойному персептрону, очень ограничен. Рассмотрим однослойную сеть из одного нейрона (рис).

Рис.. Сеть из одного нейрона

Выход сети задается функцией y = F (w ₁ x ₁ + w ₂ x ₂ - q). Если F имеет вид жесткой ступеньки с двумя возможными значениями, 0 и 1, то выход сети будет иметь вид (рис.).

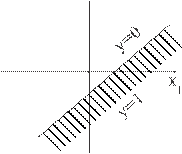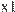Рис.. Решающая поверхность однослойного персептрона

Гиперплоскость (в случае многих входов), разделяющая различные значения выхода, называется решающей поверхностью. Для жесткой ступеньки решающая поверхность задается уравнением:

w ₁ x ₁ + w ₂ x ₂ = q

Для двухвходового нейрона она имеет вид прямой, произвольно повернутой и смещенной из начала координат. Угол поворота определяется коэффициентами w ₁, w ₂, а смещение из начала координат — порогом q.

Если выбрана гладкая функция активации, то выход сети будет плавно меняться от нуля до единицы в направлении, перпендикулярном прямой.

Дата добавления: 2014-01-06