Трехслойный персептрон

Трехслойный персептрон является наиболее общим в своем классе сетей и способен формировать произвольные многоугольные невыпуклые многосвязные области. Нейроны первых двух слоев создают произвольные независимые многоугольные решающие области в нужном количестве и в нужных измерениях входного пространства X. Эти области объединяются нейронами третьего слоя в нужной комбинации. Как и для двухслойного персептрона, допускаются операции пересечения и объединения. Весовые коэффициенты могут быть отрицательными, и соответствующая область может входить со знаком минус, что реализует операцию инверсии. Результирующая область может быть открытой.

Пример решающей области для жесткой нелинейности в нейронах показан на рис.. Первый и второй слой формируют независимые подобласти S₁, S₂, S₃. Единственный нейрон третьего слоя объединяет их по закону (S ₁ Ú S ₃) Ù Ø S ₂. Весовой коэффициент нейрона в третьем слое, соответствующий подобласти S₂, имеет знак " – ", и поэтому перед областью S₂ стоит знак отрицания.

Решающая область для трехслойного персептрона с жесткой нелинейностью

Проблема функции «исключающее ИЛИ»

Наглядной иллюстрацией ограниченности для однослойного персептрона является функция "исключающее ИЛИ". Эта булева функция от двух переменных принимает значение "истина", когда значения входных переменных различны, и "ложь" — в противном случае. Другими словами она принимает значение единицы, когда один из аргументов равен единице (но не оба). Проблему можно проиллюстрировать с помощью однослойной однонейронной системы с двумя входами, показанной на рис. 2.4. Обозначим один вход через х, а другой через у, тогда все их возможные комбинации будут состоять из четырех точек на плоскости х -у, как показано на рис. 2.5. Например, точка х = 0 и у = 0 обозначена на рисунке как точка А₀.

Рис. 2.4. Однонейронная система

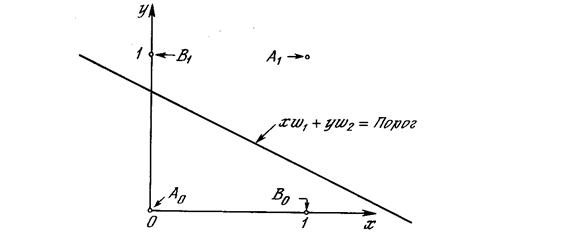
Рис. 2.5. Проблема "исключающее ИЛИ"

Табл. 2.1 показывает требуемую связь между входами и выходом, где входные комбинации, которые должны давать нулевой выход, помечены А₀ и А₁, единичный выход – В₀ и В₁.

Таблица 2.1. Таблица истинности для функции "исключающее ИЛИ"

Точки	Значения х	Значения у	Требуемый выход
A0
B0
B1
A1

В сети на рис. 2.4 функция F является обычным порогом, так что OUT принимает значение ноль, когда NET меньше 0,5, и единица в случае, когда NET больше или равно 0,5. Нейрон выполняет следующее вычисление:

NET = xw ₁ + yw ₂ (2.1)

Никакая комбинация значений двух весов не может дать соотношения между входом и выходом, задаваемого табл. 2.1. Чтобы понять это ограничение, зафиксируем NET на величине порога 0,5. Сеть в этом случае описывается уравнением (2.2).

xw ₁ + yw ₂ = 0,5 (2.2)

Это уравнение линейно по х и у, т. е. все значения по х и у, удовлетворяющие этому уравнению, будут лежать на некоторой прямой в плоскости х-у.

Любые входные значения для х и у на этой линии будут давать пороговое значение 0,5 для NET. Входные значения с одной стороны прямой обеспечат значения NET больше порога, следовательно, OUT=1. Входные значения по другую сторону прямой обеспечат значения NET меньше порогового значения, делая OUT равным 0. Изменения значений w ₁, w ₂ и порога будут менять наклон и положение прямой. Для того чтобы сеть реализовала функцию "исключающее ИЛИ", заданную табл. 2.1, нужно расположить прямую так, чтобы точки А были с одной стороны прямой, а точки В – с другой. Попытавшись нарисовать такую прямую на рис. 2.5, убеждаемся, что это невозможно. Это означает, что какие бы значения ни приписывались весам и порогу, сеть неспособна воспроизвести соотношение между входом и выходом, требуемое для представления функции "исключающее ИЛИ".

Дата добавления: 2014-01-06