
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Описание ЭВМ на уровне операционных схем и микропрограмм
|
|
|
|
ЭВМ представляется в виде совокупности взаимосвязанных операционных устройств, каждое из которых предназначено для выполнения определенного набора операций.
F= {f1, f2, …, fn}- множество операций.
A= {a1, a2, …, ap}- множество входных слов.
C= {c1, c2, …, cs}- множество выходных слов.
R= {r1, r2, …, rq}- множество внутренних слов.
{A,(B),C,F,R}

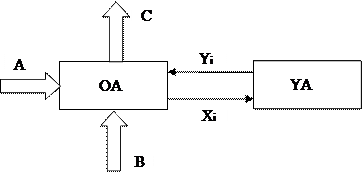
Любое ОУ можно рассматривать в виде композиции двух автоматов:
- Операционного автомата (ОА)
- Управляющего автомата (УА)
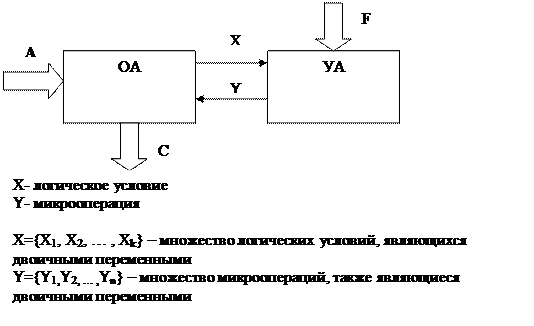
ОА имеет дело с обрабатываемыми словами, над которыми выполняется микрооперация Yi. Управляющий автомат работает по микропрограмме, которая состоит из микрокоманд.
Микрокоманда – это совокупность микроопераций, выполняемых в одном машинном такте, при работе микропрограммы.
Микрооперация – это элементное машинное действие, которое не может быть разбито на более мелкие.
Микропрограмма – это алгоритм выполнения машинной операции, описанной в терминах микроопераций и логических условий. ОА состоит из набора операционных элементов.
Для выполнения микроопераций в ОА существует схема, которая инициализируется (начинает работать) под действием соответствующего управляющего сигнала yi, поступающего из УА.
УА служит для формирования последовательности управляющих сигналов yi на основе значений логических условий, поступающих из ОА и реализуемых микропрограммой.
Операционные элементы (ОЭ)
ОА состоит из ОЭ, каждый из которых описывается:
- входными и выходными словами
- множеством реализованных микроопераций
- множеством формируемых логических условий.
Типы операционных элементов:
- Управляемая шина – служит для передачи слова информации.
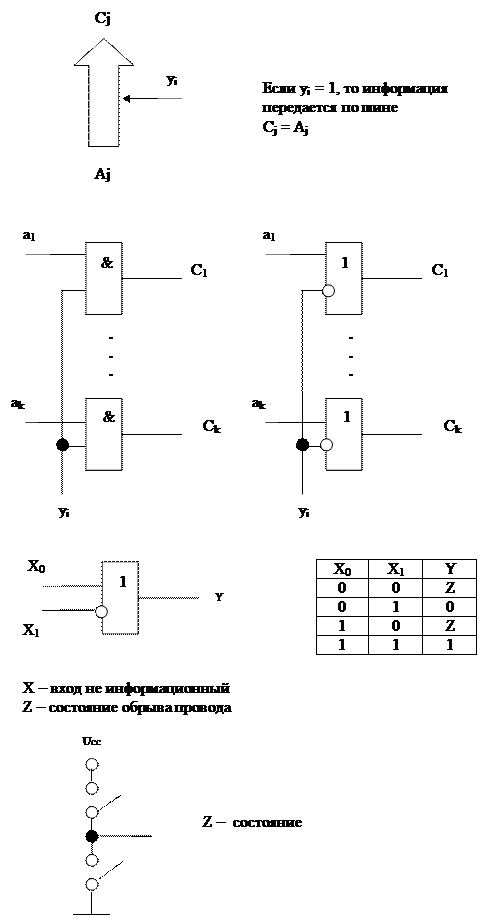
- Регистры для передачи и хранения информации.
Регистр – набор триггеров, каждый из которых хранит 1 бит информации (0 или 1)
a) регистр для хранения информации с одним выходом.
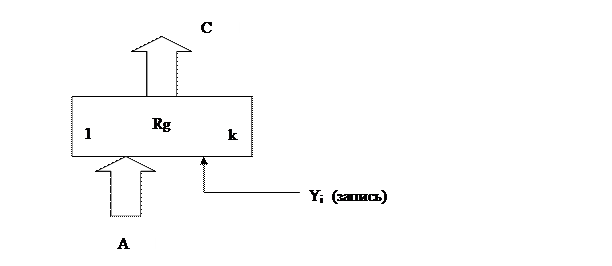
Одна микрооперация – запись.
Старший разряд регистра может использоваться в качестве логического устройства, характеризующего знак числа.
b) Регистр с двумя выходами.
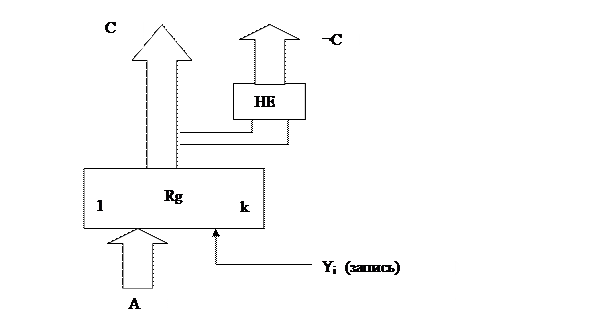
с) многофункциональный регистр

Например Y1 – сброс, Y2 – прием числа, Y3 – сдвиг содержимого на 1 разряд влево, Yk - сдвиг содержимого на 1 разряд вправо и др.
- Счетчик
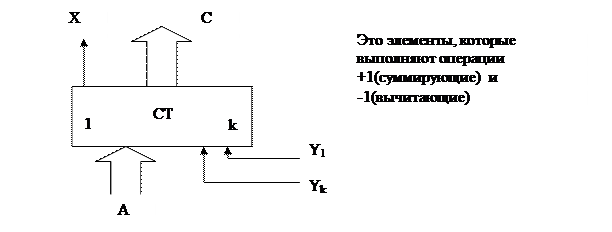
Y1 – обнуление СT: = 0
Y2 – прием кода CT:= A
Y3 – прямой счет CT:= CT + 1
Yk – обратный счет CT:= CT - 1
X – логическое условие: 0, если СТ:≠0 и 1, если СТ:=0
- Различные комбинационные узлы
a) Дешифраторы

b) Сумматоры
1. Комбинационный сумматор
Не содержит запоминающих элементов, т.е. триггеров, и предназначен для реализации микрооперации C=A+B.

Он состоит из одноразрядных сумматоров.
2. Одноразрядный сумматор
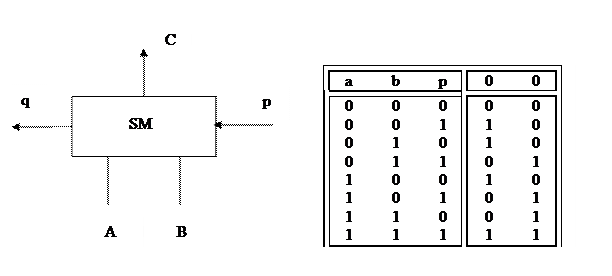
C:
| --------------p | |||||
  -----------------b -----------------b
| |||||

 0 0
|  0 0
| ||||
q:
| --------------p | |||||
| -----------------b | |||||
 0 0
|  1 1
| ||||
 1 1
|  1 1
|
После минимизации по Картам Карно получим:
q=pb v ab v ap
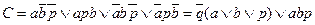
Карта Карно представляет собой форму табличной истинности. Число клеток карты = числу строк таблицы. Внутри клеток записывается значение функций. Строки и столбцы карт Карно помечаются половиной входных аргументов. Последовательность нумераций строк и столбцов соответствует координатам Грея:
|
Если теперь построить схему, то получим:
|

|
|
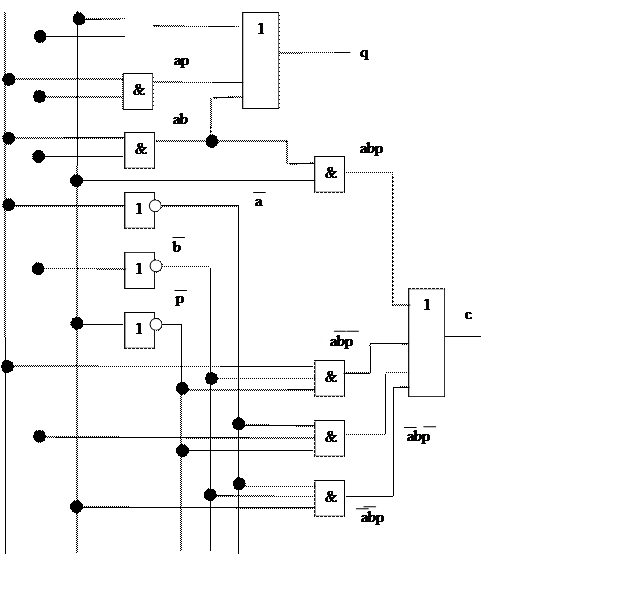
2. Накапливающий сумматор.

Способы представления микропрограмм.
Для описания микропрограмм используют три различных языка:
1. язык графической схемы алгоритма ГСА
2. язык логической схемы алгоритма ЛСА
3. язык метрической схемы алгоритма МСА
ГСА - это ориентированный граф, в котором используются следующие вершины:

|
начальной микрооперацией У0. Имеет только один выход.
 | |||||
 | |||||
|

- конечная вершина, получаемая Ук. Может иметь несколько входов.
|
 - операторная вершина, получаемая Уi. Может иметь несколько
- операторная вершина, получаемая Уi. Может иметь несколько
входов и один выход.
и один выход.

|

 - логическая вершина. Имеет несколько входов и только два
- логическая вершина. Имеет несколько входов и только два
выхода, отмеченные некоторыми значениями переменной Xi.
Алгоритмы бывают:
- линейные,
- разветвляющиеся,
- циклические.
а) линейный алгоритм. б) разветвляющийся алгоритм.






|


|
|

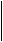






|
|
|


|
 | |||||
 | |||||
 |
в) циклический алгоритм.
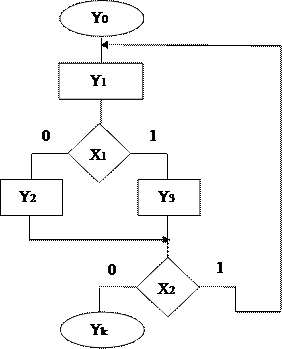
Условия корректности ГСА:
1. достижимость – должен существовать путь из начальной вершины в любую операторную.
2. отсутствие тупиковых ситуаций – должен существовать путь из каждой операционной вершины в конечную.
Достоинства и недостатки:
Достоинства ГСА – наглядность.
Недостатки ГСА – громоздкость,
- сложность представления в машинных кодах.
ЛСА – это строчная запись операторов алгоритма:
- Y0, Yk – начальная и конечная вершины алгоритма.
- Yi – операторная вершина
- Xj – оператор логического условия.
Пример: Xj└q ┘q
Если значение Xj = 0, то переходим к оператору, стоящему за закрывающей полускобкой, а если Xj=1, то за открывающей полускобкой.
Для задания безусловного перехода используется тождественно ложный логический оператор: Om└n ┘n
Пример:
Линейный алгоритм (см.выше): Y0Y1Y2…Yk
Разветвляющийся алгоритм: Y0Y1X1 └5 X2└7 Y4 O1└1 ┘5 Y2O2└4 ┘7 Y3┘1 ┘4Yk
МСА – это квадратная матрица, строки которой помечены операторами от Y0 до Yk-1, а столбцы матрицы, помечены операторами от Y1 до Yk. На пересечении i-ой строки и j-го столбца записывается условия достижимости оператора Yj из оператора Yi.
Линейный алгоритм (см. выше).
| Y1 | Y2 | .... | Yk | |
| Y0 | ||||
| Y1 | ||||
| . . . | . . . | |||
| Yk-1 | ||||
Начальная вершина – микрон Y0.
Переход из Yi Yj - 1
Разветвляющийся алгоритм (см. выше).
| Y1 | Y2 | Y3 | Y4 | Yk | |
| Y0 | |||||
| Y1 |  X1 X1
|  X1 X2 X1 X2
| X1 X2 | ||
| Y2 | |||||
| Y3 | |||||
| Y4 |
 |
 X1 v X1 X2 v X1 X2
X1 v X1 X2 v X1 X2
Условия корректности:
1. Отсутствие пустых строк и столбцов.
2. В каждой строке объединение по «или» всех логических условий должно приводить к 1.
3. Эти два условия одновременно проверяют достижимость оперативных вершин и наличие пути из них в конечную.
Достоинства: удобно хранить в памяти компьютера.
Недостатки: очень громоздок, при большом количестве операторов.
Операционное устройство для выполнения операций алгебраического сложения двоичных чисел.
Способы кодирования чисел со знаком:
| Прямой | Обратный | Дополнит. | |
| +23 | |||
| -23 | |||
| +18 | |||
| -18 |
- «1»
+ «0»
модуль 23= 10111
модуль 18= 10010
При прямом кодировании отрицательного и положительного числа отличается лишь знаком и не отличается модулем.
В обратном коде: положительные числа совпадают с прямым, отрицательные – инвертируются.
В дополнительном коде: положительные – совпадают с прямым, в отрицательном числе – инвертируются прям +1
Знак числа кодирования «+» - «0»,«-» - «1» во всех способах кодирования.
Если при выполнении операции выбирается способ кодирования (прямой, обратный или дополнительный), то как отрицательное, та и положительное число представляет собой только в выбранном способе кодирования.
Положительные числа при прямом, обратном и дополнительном кодировании имеют один и тот же вид.
Суммирование при использовании прямого кодирования.
Алгоритм выполнения суммирования сложения:
Он подразумевает предварительный анализ знаков и анализ модулей.
Ищем число с большим модулем и его приписывается к знаку результата. Если знак второго числа совпадает, то выполняется суммирование, если не совпадает – из большего вычитается меньшее.
| +23 | |
| -18 | |

| |
| -23 | |
| +18 | |

|
23>18
→ +5
23>18
→ -5
Суммирование чисел при использовании обратного кода.
При данном способе осуществляется безусловное суммирование всех разрядов числа знаковые, перенос из старшего разряда прибавляется к результату суммирования.
Сумма получается в обратном виде:
 +23 1 010111
+23 1 010111

 -18 101101
-18 101101
 000100
000100
 |
000101 → +5 в обратном коде.
 |
-23 0 101000
 +18 000010
+18 000010

 111010 → -5 в обратном коде.
111010 → -5 в обратном коде.
Осуществляется безусловное суммирование всех разрядов, а результат в дополнительном коде.
 Дополнительный код.
Дополнительный код.
+23 1 010111
 -18 101110
-18 101110
000101 → +5 в дополнительном коде.
-23 101001
 +18 101110
+18 101110
111011 → -5 в дополнительном коде.
Суммирование в дополнительном коде наиболее быстрое, в прямом коде самые медленные. Использование обратного кодирования позволяет производить преобразования из прямого в обратное и наоборот.
|
|
|
|
|
|






23 010111
18 010010 переполнение разряда сети



 101001
101001
Используются модифицированные разряды.
00 +
11 -
|
 01 +
01 +
10 -
Модифицированный код.
При суммировании чисел с одним знаком возможна ситуация, когда результат не вмещается в разрядность модуля (предыдущий пример).
Получают число с обратным знаком. Чтобы легко выявить такие ситуации используют модифицированный знаковый разряд, когда под знаковый разряд отводят два разряда 00 – положительное число, 11 – отрицательное число.
В случае переполнения, получается 01, 10, причем старший бит соответствует правильному значению знака, а младший показывает о наличии переполнения, 10 – отрицательное переполнение.
+23 0010111
+18 0010010

 0101001 положительное переполнение.
0101001 положительное переполнение.
-23 1101000
 1100101
1100101

 1 1010101
1 1010101
 1010110 переполнение
1010110 переполнение
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 398; Нарушение авторских прав?; Мы поможем в написании вашей работы!