Перевод чисел из двоичной системы счисления

в систему счисления с основанием 2 ⁿ и обратно

Если основание n -ичной системы счисления является степенью числа 2, то перевод чисел из двоичной системы счисления в n -ичную и обратно можно проводить по более простым правилам.

Пусть q = 2³ и дано некоторое двоичное число

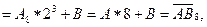
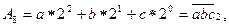
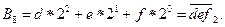
Исходя из приведенных выше рассуждений, можно сформулировать следующий алгоритм перевода целых двоичных чисел в систему с основанием q = 2 ⁿ:

Для того чтобы целое двоичное число записать в системе счисления с основанием q = 2 ⁿ, нужно:

1) данное двоичное число разбить справа налево на группы по п цифр в каждой;

2) если в последней левой группе окажется меньше п разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;

3) рассмотреть каждую группу как n -разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2 ⁿ.

Пример 1. Число 1011000010001l0010₂ заменим равным ему числом восьмеричной системы счисления.

Разбиваем число справа налево на триады (группы по 3 цифры) и под каждой из них записываем соответствующую восьмеричную цифру:

Получаем восьмеричное представление исходного числа: 541062₈.

Пример 2. Число 1000000000111110000111₂ переведем в шестнадцатеричную систему счисления.

Разбиваем число справа налево на тетрады (группы по четыре цифры) и под каждой из них записываем соответствующую шестнадцатеричную цифру:

			F

Получаем шестнадцатеричное представление исходного числа: 400F87₁₆.

Для того чтобы дробное двоичное число записать в системе счисления с основанием q = 2 ⁿ, нужно:

1) данное двоичное число разбить слева направо на группы по п цифр в каждой;

2) если в последней правой группе окажется меньше п разрядов, то ее надо дополнить справа нулями до нужного числа разрядов;

3) рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2 ⁿ.

Пример 3. Число 0,10110001₂ заменим равным ему числом восьмеричной системы счисления.

Разбиваем число слева направо на триады и под каждой из них записываем соответствующую восьмеричную цифру:

000,
0,

Получаем восьмеричное представление исходного числа: 0,542₈.

Пример 4. Число 0,100000000011₂ переведем в шестнадцатеричную систему счисления. Разбиваем число слева направо на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:

0,
0,

Получаем шестнадцатеричное представление исходного числа: 0,803₁₆.

Для того чтобы произвольное двоичное число записать
в системе счисления с основанием q = 2ⁿ, нужно:

1) целую часть данного двоичного числа разбить справа налево, а дробную - слева направо на группы по п цифр в каждой;

2) если в последней левой и/или правой группе окажется меньше п разрядов, то их надо дополнить слева и/или справа нулями до нужного числа разрядов;

3) рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2ⁿ.

Пример 5. Число 111100101,0111₂ заменим равным ему числом восьмеричной системы счисления.

Разбиваем целую и дробную части числа на триады и под каждой из них записываем соответствующую восьмеричную цифру:

		101,
		5,

Получаем восьмеричное представление исходного числа: 745,34₈.

Пример 6. Число 1001000,1101001₂ переведем в шестнадцатеричную систему счисления. Разбиваем целую и дробную части числа на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:

	1000,
	8,	D

Получаем шестнадцатеричное представление исходного числа: 48,D2₁₆.

Для того чтобы произвольное число, записанное в системе счисления с основанием q = 2ⁿ, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее
n -значным эквивалентом в двоичной системе счисления.

Пример 7. Переведем шестнадцатеричное число 4AC35 в двоичную систему счисления. В соответствии с алгоритмом:

	A	C

Получаем двоичное представление исходного числа:

1001010110000110101₂.

Пример 8. Переведем восьмеричное число 1024₈ в двоичную систему счисления.

Получаем двоичное представление исходного числа:

1000010100₂.

Описанные алгоритмы позволяют достаточно быстро и просто осуществлять переводы десятичных чисел в двоичную систему счисления и обратно с использованием в качестве промежуточной восьмеричной или шестнадцатеричной системы счисления.

Дата добавления: 2014-01-06