Методы количественного анализа систем

Все задачи принятия решений можно разбить на задачи в условиях определенности, в условиях риска и условиях неопределенности.

К классу задач принятия решений в условиях определенности относятся задачи, для решения которых имеется достаточная и достоверная количественная информация. Тогда можно применять методы математического программирования.

Задачи принятия решений в условиях риска имеют место, если все возможные исходы операций можно описать с помощью некоторого вероятностного распределения для построения распределений необходимо иметь статистические данные, либо привлекать знания экспертов. Для решения этого класса задач использую методы одномерной и многомерной полезности.

Задачи принятия решений в условиях неопределенности появляются в том случае, когда информация для принятия решений является неточной, неполной, неколичественной. В зависимости от характера неопределенности операции могут делиться на игровые и статистические. В игровых операциях неопределенность вносит своими сознательными действиями оппонент. Для исследования игровых операций используется теория игр. Условия статистически неопределенных операций зависят от объективной действительности, называемой природой. природа рассматривается как незаинтересованная, безразличная к операции (она пассивна по отношению к лицу, принимающему решение). Такие операции могут исследоваться с применением теории статистических решений.

Рассмотрим применение математических методов и моделей к количественным моделям принятия решений. В основу классификации, показанной в таблице 4.1, положены признак достоверности информации (определенность – риск - неопределенность) и временной фактор (статика - динамика).

Таблица 4.1 – Математические методы принятия решений

	Определенность	Риск	Неопределенность
Несколько лиц	Незнание	Несколько критериев
Статика	Линейное программирование	Стохастическое программирование	Теория игр	Статистические решения	Многокритериальная оптимизация
Нелинейное программирование	Теория полезности
Параметрическое программирование	Групповые решения
Дискретное, в том числе целочисленное программирование	Антогонистичесике игры	Игры с природой	Игры с природой
Геометрическое программирование	Теория нечетких множеств
Динамика	Вариационное исчисление	Стохастическое динамическое программирование	Теория позиционных игр	Теория обучения	Многоцелевая оптимизация в функциональных пространствах
Оптимальное управление
Динамическое программирование	Массовое обслуживание
Сетевое планирование	Управление случайными процессами	Игры на случайных процессах	Статистические решения
Математическое программирование в функциональных пространствах

Методы принятия решений наиболее хорошо разработаны для задач «статика-определенность». Особенно распространенными являются алгоритмы линейного программирования. Для решения задач нелинейного программирования используют линейного аппроксимацию для того, чтобы применить алгоритмы линейного программирования.

Стохастическое программирование позволяет дополнительно учесть вероятностные факторы.

Вопросы решения статических задач при неопределенной исходной информации рассматриваются в теории игр, теории статистических решений, методах многокритериальной оптимизации, теории нечетких множеств.

Методы типа динамика - определенность в основном предназначены для решения технологических и технико-экономических задач.

Стохастическое динамическое программирование и управление сложными процессами относятся к динамическому программированию и оптимальному управлению, так же как стохастическое программирование к математическому программированию. Методы массового обслуживания предназначены для анализа систем обслуживания случайно возникающих требований.

Методы типа динамика - неопределенности и динамики мало отличаются от методов типа статика – неопределенность. Однако здесь гораздо больше технологических требований. Требуется корректная формулировка некоторых задач и их решение требует достаточно высокой математической подготовки.

В задачах прогнозирования социально-экономических процессов преобладающим инструментарием являются статистические и эконометрические методы, методы имитационного моделирования.

Первоначально задача количественного анализа систем формулировалась в терминах критерия превосходства в форме:

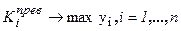. (4.1)

Однако поскольку большинство частных показателей качества связаны между собой так, что повышение качества по одному показателю ведет к понижению качества по другому, такая постановка была признана некорректной для большинства практических важных приложений [1].

Наличие неоднородных связей между отдельными показателями сложных систем приводит к проблеме корректности критерия превосходства и к необходимости идти на компромисс и выбирать для каждой характеристики не оптимальное значение, а меньшее, но такое, при котором и другие показатели тоже будут иметь приемлемые значения.

Для решения проблемы корректности критерия превосходства были разработаны методы количественной оценки систем:

- методы теории полезности;

- методы многокритериальной оптимизации;

- методы ситуационного управления.

Методы теории полезности основаны на аксиоматическом использовании отношения предпочтения множества векторных оценок систем.

Методы многокритериальной оптимизации базируются на эвристическом использовании понятия векторного критерия качества систем (многокритериальные задачи) и включают методы главного критерия, лексикографической оптимизации, последовательных уступок, скаляризации, человеко-машинные и другие методы.

Методы ситуационного управления, инженерии знаний основаны на построении семиотических моделей оценки систем. В таких моделях система предпочтений ЛПР формализуется в виде набора логических правил, на котором может быть осуществлен выбор альтернатив. При этом понятие векторного критерия в явном виде не используется.

Дата добавления: 2014-01-06