Методы теории полезности

При аксиоматическом подходе к оценке систем на основе теории полезности [1] используют метод свертывания векторного пространства в скалярный. Отличие данного метода от остальных заключается в том, что свертывание производится на основе аксиоматизации предпочтений ЛПР.

Выявить формально отношений предпочтения или безразличия непосредственным сравнением альтернатив затруднительно: показатели исходов операций многочисленны, имеют разный физический смысл и разные шкалы измерения. Отношение к альтернативам выражают в количественной форме, приписывая каждому исходу некоторое число, определяющее его относительную предпочтительность. Например, наименее полезный исход может быть отражен числом 1, следующий числом 2 и т.д. до наиболее полезного исхода.

Таким образом, полезность исхода операции – это действительное число, приписываемое исходу операции и характеризующее его предпочтительность по сравнению с другими альтернативами относительно цели.

Зная возможные альтернативы с их показателями полезности, можно построить функцию полезности, которая дает основу для сравнения и выбора решений. Функция полезности представляет собой числовую ограниченную функцию U(a), определенную на множестве альтернатив A={a_k}, k=1,2,…,n, так, что U(a_i) = U(a_j), когда альтернативы a_i и a_j неразличимы (a_i ~ a_j), т.е нельзя отдать предпочтение ни тому, ни другому исходу, и U(a_i)>U(a_j), когда альтернатива a_i предпочтительнее a_j ().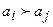

В теории полезности доказывается существование функции полезности в виде отображения упорядоченного множества альтернатив А в множество действительных чисел U: A→R¹. Предпочтения ЛПР формулируются в виде аксиом. Поскольку системы предпочтения у разных ЛПР могут различаться, то разные аксиоматики приводят в различным видам свертки, и следовательно, функция полезности не единственна.

Согласно теории полезности в реальной задаче оценки систем при определенных условиях существует функция полезности, однозначно определенная на множестве всех альтернатив с точностью до монотонного строго возрастающего линейного преобразования.

Процедура определения функции полезности включает три основных этапа:

- выявление показателей исходов (альтернатив) операции,

- определение множества допустимых исходов операции,

- определение полезности исходов операции.

Определение полезности как меры оценки того или иного исхода операции представляет сложную задачу, точные методы решения которой пока не найдены. Все известные способы определения функции полезности носят приближенный характер и строятся на основе анализа влияния исходов исследуемой операции на операцию более высокого уровня иерархии, экспертных оценок и аппроксимации.

Дата добавления: 2014-01-06