Дерево решений

(дополнительная информация для самостоятельной работы)

Теория полезности экспериментально исследовалась в так называемых задачах с вазами (или урнами) [10]. Ваза - это непрозрачный сосуд, в котором находится определённое (известное лишь организатору эксперимента) количество шаров различного цвета. Задачи с вазами типичны для группы наиболее простых задач принятия решений – задач статистического типа (см. также раздел «Статистические игры»).

Человек делает выбор в этих задачах, основываясь на расчётах. Варианты действий выражены в наиболее простом виде.

Типовая задача для испытуемого может быть представлена следующим образом.

Перед испытуемым ставится ваза, которая может быть вазой 1-го или 2-го типа. Даётся следующая информация: сколько имеется у экспериментатора ваз 1-го и 2-го типов; сколько черных и красных шаров в вазах 1-го и 2-го типов; какие выигрыши ожидают испытуемого, если он угадает, какого типа ваза; какие проигрыши ожидают его, если он ошибётся. После получения такой информации испытуемый должен сделать выбор: назвать, к какому типу принадлежит поставленная перед ним ваза.

Пусть, например, экспериментатор случайно выбирает вазу для испытуемого из множества, содержащего 700 ваз 1-го типа и 300 ваз 2-го типа. Пусть в вазе 1-го типа содержится 6 красных шаров и 4 чёрных. В вазе 2-го типа содержится 3 красных и 7 чёрных шаров.

Если перед испытуемым находится ваза 1-го типа и он угадает это, то получит выигрыш 350 денежных единиц (д.е), если не угадает, его проигрыш составит 50 д.е. Если перед ним ваза 2-го типа и он это угадает, то получит выигрыш 500 д.е., если не угадает, его проигрыш составит 100 д.е. Испытуемый может предпринять одно из следующих действий: d₁- сказать, что ваза 1-го типа; d₂- сказать, что ваза 2-го типа. Условия задачи можно представить в таблице 4.1.

Таблица 4.1 - представление задачи с вазами

Тип вазы	Вероятность выбора вазы данного типа	Выигрыш при действии
d1	d2
	0,7		-100
	0,3	-50

Необходимо оценить среднюю (ожидаемую) полезность каждого из действий и выбрать действие с максимально ожидаемой полезностью. В соответствии с этой рекомендацией мы можем определить среднее значение выигрыша для каждого из действий:

U (d₁)=0,7*350 - 0,3*50=230 д.е;

U (d₂)= 0,3*500 - 0,7*100=80 д.е.

Следовательно, разумный человек выберет действие d1, а не действие d2.

Из этого примера следуют общие рекомендации действий для рационального человека: определить исходы, помножить их на соответствующие вероятности, получить ожидаемую полезность и выбрать действие с наибольшей полезностью.

Приведенная выше таблица 2 может быть представлена в виде дерева решений, представленного на рисунке 4.1. На этом дереве квадрат означает место, где решение принимает человек, а круг - место где всё решает случай. На ветвях дерева написаны значения вероятностей, а справа у конечных ветвей - значения исходов (результаты).

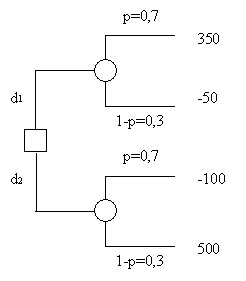
Рисунок 4.1 – Дерево решений

Дерево решений можно использовать для представления всех возможных действий и для нахождения последовательности правильных решений, ведущих к максимально ожидаемой полезности. Для того, чтобы это продемонстрировать, усложним задачу.

Предоставим человеку, выбирающему между действиями d₁ и d₂, дополнительные возможности. Пусть он может до своего ответа вытащить за определённую плату один шар из вазы, причём после вытаскивания шар кладётся обратно в вазу. Плата за вытаскивание одного шара 60 д.е Дерево решений с двумя его основными ветвями представлено на рисунке 4.2. Теперь вопрос о том, какое решение следует принимать, стал сложнее: необходимо решить, стоит ли вынимать шар и какой ответ дать после вытаскивания красного или чёрного шара. При принятии решений применим способ подсчёта изменения вероятностей событий после получения дополнительной информации.

Итак, вероятность вытащить красный шар из вазы 1-го типа p_k(B1)=0,6, а из вазы 2-го типа p_k(B2)=0,3. Зная все условные вероятности (зависящие от условия), а так же вероятности p₁ и p₂ выбора ваз 1-го и 2-го типа (таблица 4.1), поставим следующие вопросы.

1. Рассчитаем эти вероятности:

p_k (B1)= 0,7*0,6= 0,42, если ваза окажется 1-го типа,

p_k (B2)= 0,3*0,3= 0,09, если ваза окажется 2-го типа.

Следовательно, вероятность вытащить красный шар в общем случае:

p_k = p_k (B1) + p_k (B2) = 0,51.

Аналогичным образом можно подсчитать, что вероятность вытащить чёрный шар p_ч=0,49.

2. Пусть вытащенный шар оказался красным (чёрным). Какое действие следует выбрать: d₁ или d₂? Для ответа на этот вопрос нужно знать вероятности принадлежности ваз к 1-му и 2-му типам после получения дополнительной информации. Эти вероятности позволяет определить формула Байеса.

Например, мы вытащили красный шар. Какова после этого вероятность того, что перед нами стоит ваза 1-го типа? Приведём все обозначения вероятностей:

p_k(B₁) - вероятность вытащить красный шар из вазы 1-го типа;

p_ч(B₁) - вероятность вытащить чёрный шар из вазы 1-го типа;

p_k(B₂) - вероятность вытащить красный шар из вазы 2-го типа;

p_ч(B₂) - вероятность вытащить чёрный шар из вазы 2-го типа;

p(B₁) - вероятность того, что ваза 1-го типа

p(B₂) - вероятность того, что ваза 2-го типа;

p(B_1/k) - вероятность того, что ваза окажется 1-го типа после вытаскивания красного шара;

p(B_1/ч) - вероятность того, что ваза окажется 1-го типа после вытаскивания чёрного шара;

p(B_2/k) - вероятность того, что ваза окажется 2-го типа после вытаскивания красного шара;

p(B_2/ч) - вероятность того, что ваза окажется 2-го типа после вытаскивания чёрного шара.

Формула Байеса позволяет оценить p(B_i/k) p(B_i/ч), где i=1,2, используя все прочие вероятности:

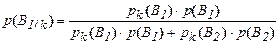. (4.2)

Для решаемой задачи p(B_1/k)= 0,82; p(B_1/ч)= 0,57; p(B_2/k)=0,18; p(B_2/ч)=0,43.

Теперь имеем всю информацию, необходимую для принятия решений.

На рисунке 4.2 показаны две основные ветви дерева решений, причём верхняя повторяет дерево решений на рисунке 4.1. Квадрат 1 слева соответствует первому решению - вытаскивать шар или нет. Случаю отказа от вытаскивания шара соответствует нижняя ветвь, начинающаяся со случайного события (круг). В квадратах 2,3,4 принимаются решения о выборе одной из двух стратегий: d₁ или d₂. Далее всё решает случай (круги).

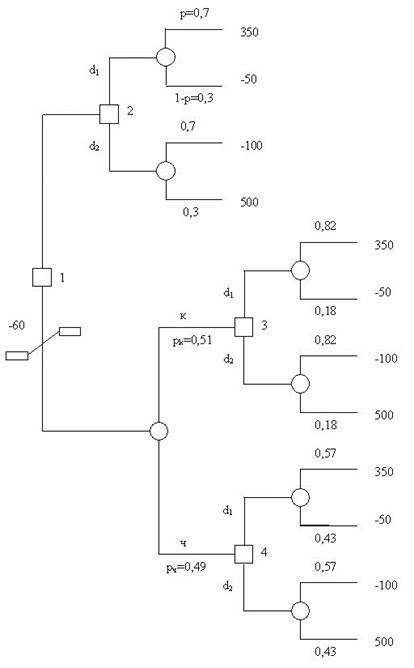
Рисунок 4.2 – Дерево решений

Существует три простых правила выбора оптимальной (по критерию максимума ожидаемой полезности) последовательности решений на основе дерева решений.

1) идти от конечных ветвей к его корню;

2) там, где есть случайность (кружок), находится среднее значение;

3) там, где есть этап принятия решений (квадратик), выбирается ветвь с наибольшей ожидаемой полезностью, а другая отсекается двумя чёрточками

Применим эти правила к дереву решений, представленному на рисунке 4.2. В результате получим дерево решений, показанное на рисунке 4.3.

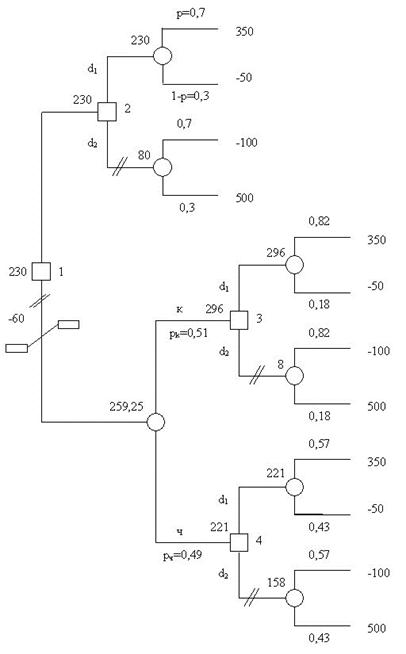
Рисунок 4.3 – «Сворачивание» дерева решений

На этом рисунке над кругами указаны средние значения полезности, двумя чёрточками отсечены ветви с меньшим значением ожидаемой полезности. Наилучший вариант действий: шар не вытаскивать и выбирать действие d₁. Этот вариант соответствует самому верхнему пути дерева решений на рисунка 4.3. Такая процедура нахождения оптимального пути на деревьях решений получила название «сворачивание» дерева решений.

Деревья решений при заданных числовых значениях вероятностей и исходов позволяют осуществить выбор той стратегии (последовательности действий), при которой достигается наибольший выигрыш, т.е. достигается максимум функции полезности ЛПР.

Дата добавления: 2014-01-06