Понятие о системах счисления

Введение

Формы представления данных в ЭВМ.

Единицы измерения информации.

Понятие о системах счисления.

Введение.

ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ЭВМ

Формирование Учетной политики.

Учетная политика организации - это выбранная ею совокупность способов ведения БУ- первичного наблюдения, стоимостного измерения, текущей группировки и итогового обобщения фактов хоз. деятельности.

Формируется руководителем, оформляется приказом до 1 января следующего года. Способы ведения БУ применяются с 1 января этого года. для вновь созданной организации не позднее 90 дней со дня ее регистрации как юридического лица.

В нее могут вноситься изменения, связанные с изменением законодательства РФ, разработки новых способов ведения БУ, существенного изменения в деятельности а/организации.

Подробнее см. Методические разработки и учебник.

Выводы.

ЛИТЕРАТУРА

1. Информатика: Учебник / Под ред. проф. Н.В.Макаровой. – М.: Финансы и статистика, 2001. Глава 4.

ЭВМ предназначены для ввода, хранения, обработки, передачи и отображения разнообразных данных, представляющих числа, текст, графику, звуки, видео и т.п. Известно, что практически все цифровые ЭВМ имеют дело с двоичными данными, т.е. данными, представляемыми последовательностями нулей и единиц. Для человека привычным является десятичное представление числовых данных, использование символов алфавита родного языка для выражения на бумаге своих мыслей и т.д. Возникает вопрос: как с помощью 0 и 1 выразить все многообразие окружающего нас мира и представить данные в ЭВМ.

Цель данной лекции заключается в ознакомлении студентов с формами представления разнообразных данных в персональных компьютерах.

Система счисления — это способ записи чисел с помощью ограниченного набора специальных знаков (цифр).

Как правило, в качестве цифровых знаков используются арабские и римские цифры.

Системы счисления подразделяются на позиционные и непозиционные.

В непозиционных системах счисления вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Примером непозиционной системы счисления является римская. Она включает в следующие цифровые обозначения: 1 – I, 2 – II, 3 – III, 4 – IV, 5 – V, 6 – VI, 7 – VII, 8 – VIII, 9 – IX, 10 – X, 50 – L, 100 – C, 500 – D, 1000 – M и т.д.

Пример 1. Записать числа 114, 155, 1999, 2005.

114 – CXIV; 155 – CLV; 1999 – MCMXCIX; 2005 – MMV.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.

В позиционной системе счисления с основанием р (в качестве которого можно принять любое натуральное число — два, три, четыре и т.д.) числа представляются в виде последовательности цифровых знаков:

(1)

где a_i – одна из допустимых цифр системы счисления по основанию р, находящаяся на i -й позиции; n и m – число целых и дробных разрядов числа, соответственно.

Максимальное целое число, которое может быть представлено в n разрядах, равно 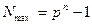, а минимальное значащее (не равно 0) число, которое можно записать в m разрядах дробной части, равно .

Имея в целой части числа n, а в дробной m разрядов, можно записать всего 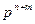разных чисел.

В информатике широко применяются десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления (табл. 1).

Таблица 1. Системы счисления, применяемые в информатике

Основание системы счисления	Название	Используемые цифры	Сфера применения
	десятичная	{0,1,2,3,4,5,6,7,8,9}	Математика
	двоичная	{0,1}	Внутреннее представление данных в узлах ЭВМ
	восьмеричная	{0,1,2,3,4,5,6,7}	Программирование
	шестнадцатеричная	{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}	Программирование

Пример 2. Представить числа в рассмотренных системах счисления в виде разложения (1):

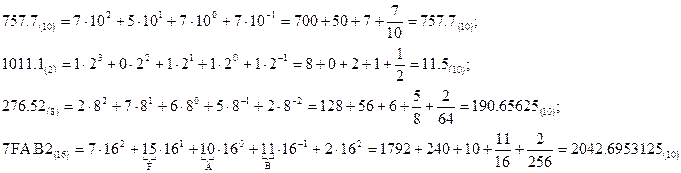
В любой позиционной системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д. Продвижением цифры называют замену её следующей по величине, т.е. продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.

Целые числа в любой системе счисления порождаются с помощью правила счета:

Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.

Применяя это правило, запишем первые двадцать целых чисел в разных системах счисления (табл. 2).

Таблица 2. Представление целых чисел в разных системах счисления

Система счисления
Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
			A
			B
			C
			D
			E
			F

Выбор числа 10 в качестве основания системы счисления исторически связан с числом пальцев на руке человека (правда, в Китае до недавнего времени использовалась пятеричная система счисления). Однако десятичная система счисления не является наиболее удобной с точки зрения ее реализации в ЭВМ. Любой из символов, применяемых при записи чисел, должен в ЭВМ изображаться в виде одного из нескольких возможных состояний некоторого физического элемента. Естественно, что эти состояния должны быть устойчивы и четко различимы.

Выполнение элемента с десятью четко различимыми состояниями представляет собой сложную техническую задачу, в то время как элементов с двумя четко различимыми состояниями имеется достаточно много (замкнутый или разомкнутый контакт, открытый или закрытый транзистор, намагниченный или размагниченный магнитный носитель и т.п.). Указанное обстоятельство явилось одной из главных причин широкого распространения двоичной системы счисления в вычислительной технике.

Важным преимуществом двоичной системы является простота выполнения арифметических и логических операций.

Однако двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Поэтому программисты в целях компактности записей используют восьмеричную и шестнадцатеричную системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 – соответственно, третья и четвертая степени числа 2), а правила перевода чисел из двоичной системы в восьмеричную (шестнадцатеричную) или наоборот чрезвычайно просты.

Дата добавления: 2014-01-06