Простейшие приближенные методы теории переноса нейтронов и -квантов

Строгое решение уравнения переноса (1) встречает непреодолимые математические трудности. На практике используют либо численное моделирование задач переноса методом Монте-Карло, либо такие приближенные аналитические методы, как методы моментов, групп, сферических гармоник, диффузионное приближение и др. Рассмотрим лишь некоторые простейшие методы, получившие применение при решении задач радиоактивного каротажа.

Простейшие формулы для распределения γ-квантов

Поток частиц от точечного источника в пустоте обусловлен лишь мощностью (интенсивностью) 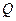(с^-1) источника и геометрическим фактором, т.е. их расхождением по поверхности сферы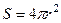

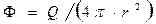(4)

Для потока - излучения в единицах мощности экспозиционной дозы на расстоянии r пользуются несколько иной формулой

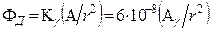(5)

где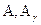— соответственно активность источника (в Бк) и его γ-активность в мг-экв.Ra; 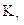— γ -постоянная изотопа, равная мощности дозы, создаваемой источником в 1 Бк на расстоянии 1м.

Поток частиц при чистом поглощении или в общем случае поток 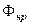нерассеянной составляющей излучения от точечного источника обусловлен как взаимодействием со средой, так и геометрическим расхождением. Формулу для Ф получают суперпозицией выражений 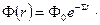и (4):

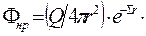(6)

Поток частиц с учетом вклада рассеянной составляющей можно представить в виде

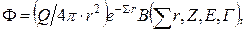(7)

где В - фактор накопления для потока излучения; Г - формальное обозначение геометрии задачи.

Выражение (7) чаще всего используется в теории переноса 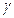- квантов. В этом случае вместо фактора накопления В практически предпочитают пользоваться энергетическими Вэ или дозовыми В_Д факторами, равными соответственно отношению общей энергии (дозы) излучения к энергии (дозе) его нерассеянной составляющей. Экспериментально, а также численными методами изучена зависимость фактора 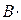от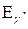 и µ _оr, где µ_о — значение µ при начальной энергии γ-квантов (для γ-квантов макроскопическое сечение 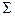принято обозначать 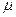). Пример соответствующих зависимостей приведен на рис. 7.

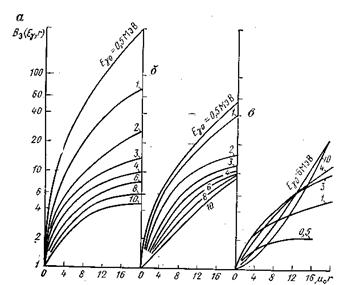
Рис.7 Энергетические факторы накопления В_э γ - излучения при прохождении через воду(а), железо(б), свинец(в).

При аналитических расчетах зависимость 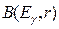для точечного источника аппроксимируют различными формулами, чаще всего формулой Тейлора:

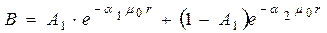(8).

дающей удовлетворительную точность до 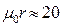Значения коэффициентов 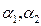зависят от вида вещества и начальной энергии 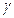- квантов, они имеются в справочниках по защите от γ-излучения.

Вклад рассеянного излучения в случае точечного источника может быть учтен также введением в формулу (7) эффективного коэффициента ослабления 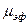вместо 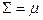аналогично тому, как это делали в выражении 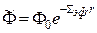для параллельного пучка. Величина 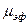в отличие от µ зависит не только от и Z, но и от r.

Диффузионное приближение

Диффузионное приближение теории переноса ядерных излучений удовлетворительно описывает пространственно-временное распределение лишь при условии, что плотность частиц не сильно изменяется по длине 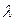свободного пробега, т.е. на расстоянии между очередными актами рассеяния. Для этого необходимо, в частности, чтобы сечение поглощения (захвата) частиц было значительно меньше сечения рассеяния .

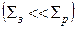При выводе уравнения диффузии предполагается также, что сечение не зависит от направления движения частиц и постоянно на всех этапах процесса переноса частицы в среде. Среднее время между двумя очередными соударениями предполагается значительно меньшим, чем время, в течение которого происходит заметное изменение распределения частиц. Кроме того, распределение частиц и их рассеяние считаются изотропными в лабораторной системе координат.

Этим условиям достаточно хорошо удовлетворяет диффузия тепловых нейтронов в слабопоглощающей среде, за исключением области вблизи границ сред, точечных источников или зон с резким повышением плотности распределения источников. Изменения сечения рассеяния в интервале преобладающих значений энергии тепловых нейтронов, как правило, малы; их рассеяние практически изотропно, а скорость изменения плотности нейтронов на расстоянии, примерно равном 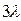, обычно невелика, за исключением областей, близких к границам сред и источникам.

Уравнение диффузии может быть выведено как приближение уравнения переноса (1). Однако поучительнее получить его другим, физически более простым способом. С произвольной точкой пространства совместим начало декартовой системы координат (рис. 8), около этой точки поместим элементарную горизонтальную площадку 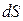Число частиц, пересекающих сверху

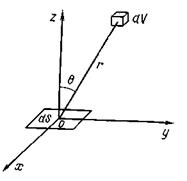
Рис. 8. Схема, поясняющая вывод уравнения диффузии

вниз площадку 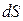можно получить как сумму (интеграл) элементарных пучков, возникших в результате рассеяния в отдельных элементарных объемах 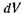верхнего полупространства и прошедших путь r до площадки 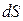без рассеяния или поглощения. Число частиц, рассеянных в объеме 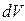за время 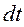, равно 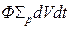, а вероятность рассеяния в телесный угол, имеющий вершину в точке расположения объема dV и опирающийся на площадку 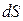, равна 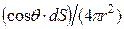Вероятность прохождения частицей пути r до площадки без взаимодействия со средой равна 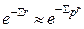, поскольку предполагаем, что , т.е. .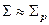

Итак, число нейтронов, пересекающих площадку 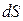сверху после соударения в произвольном элементарном объеме 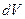, равно

.

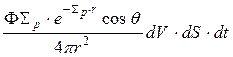Полное число нейтронов, пересекающих площадку сверху вниз, рассчитанное на единичную площадь и называемое направленной плотностью тока 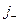, получается интегрированием по полупространству :

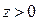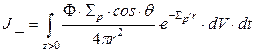
(9)

Здесь пренебрегаем временем пролета частиц от момента рассеяния до достижения площадки 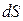и значение 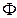для всех объемов 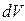берем при одном и том же времени t.

Согласно предположению о медленном изменении плотности нейтронов, представим зависимость потока в окрестности площадки 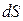в момент времени t в виде

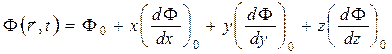(10)

Здесь нули в индексах у 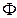и производных указывают на их вычисление в точке с координатами (0, 0, 0).

Симметрия выражения (10) по х и у приводит к тому, что при его подстановке в соотношение (9) интегралы, соответствующие второму и третьему слагаемым формулы (10), оказываются равными нулю. Поэтому после подстановки и замены z на 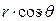выражение (9) будет иметь вид

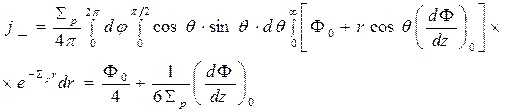(11)

Плотность тока в верхнем направлении рассчитываем аналогично, интегрируя 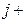по нижнему полупространству:

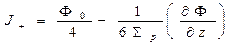
Результирующая плотность тока через площадку 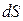перпендикулярна к оси z (плотность тока в направлении оси z),

(12)

Произвольность выбора начала и ориентации системы координат в задаче указывает на то, что плотность тока в произвольной точке г в любом направлении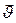

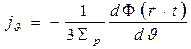
В общем случае, не изотропного рассеяния 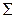меняется на 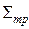, транспортное сечение :

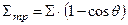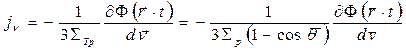(13)

Используя известную формулу, связывающую градиент скалярного поля и его производную в данном направлении, запишем:

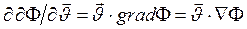
Величину

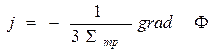(14)

называют векторным током частиц. Соотношение (14) известно как закон Фика.

Величину

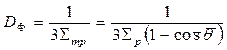
(15)

называют коэффициентом диффузии для потока частиц. Однако чаще коэффициентом диффузии (для плотности частиц) называют величину

(15а)

входящую в виде коэффициента в формулу Фика, если в ней вместо плотности потока 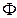стоит плотность частиц 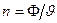т. е.

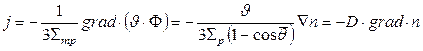(14а)

Теперь для вывода уравнения диффузии достаточно, воспользоваться соотношением баланса плотности частиц в произвольном объеме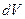

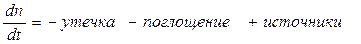. (16)

Утечка частиц в единицу времени определяется соотношением 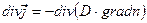Число частиц, поглощенных в единицу времени, равно 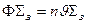. Обозначая плотность источников в единицу времени S и подставляя необходимые величины в выражение (16), получаем:

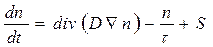(17)

где

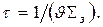(17а)

Поскольку величина 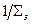согласно равенству 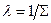представляет собой средний путь частицы до ее поглощения, величина 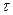будет, очевидно, средним временем жизни частиц в данной среде.

В однородной среде, или в каждой из частей пространства, состоящей из однородных сред, D =const. В таких случаях уравнение (45) будет иметь вид

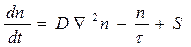(17б)

В этом случае граничные условия

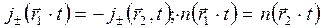
или с учетом выражения (14а)

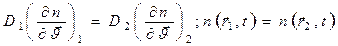
(18)

где 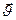— нормаль к поверхности раздела; 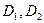— коэффициенты диффузии сред; 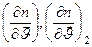— односторонние производные поля п в двух бесконечно близких точках 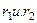на соответствующих сторонах границы раздела.

На границе среды с вакуумом ток, направленный из вакуума в среду, равен нулю (при условии, если нормаль к поверхности раздела направлена в сторону вакуума)

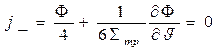(19)

Кроме того, для решения уравнения (17) необходимо задать начальные условия — распределение частиц в начальный момент времени.

Рассмотрим решение стационарного уравнения диффузии в однородной безграничной среде

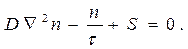(20)

Пусть источник расположен в начале сферической системы координат. Оператор Лапласа с учетом сферической симметрии задачи (независимости плотности частиц 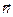от координат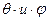) имеет вид

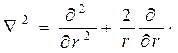
Подстановка этого выражения в соотношение (20) и учет отсутствия источников (при 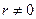) приводят к равенству

,

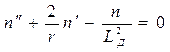где 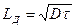— длина диффузии частиц.

При введении новой переменной и = пr последнее уравнение преобразуется так:

(21)

Общим решением уравнения (21), как известно, является функция,

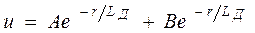(22)

где 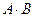— постоянные коэффициенты.

Отсюда общее решение уравнения (20)г

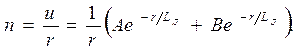
Физически очевидное условие 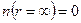требует, чтобы 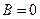Коэффициент же А легко определяется из следующего условия нормировки: суммарное число частиц во всем пространстве (нулевой пространственный момент 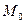) равно мощности 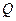источника, умноженной на среднее время жизни частиц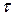

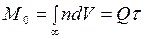(22а)

Возьмем в качестве элементарных объемов сферические слои радиусом r и толщиной 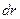и вычислим интеграл

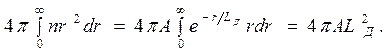(22б)

Приравнивая правые части выражений (22а) и (22б), получаем:

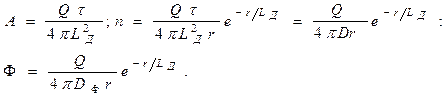(23а)

Используя решение (23), выясним физический смысл длины диффузии частиц 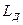. Для этого вычислим среднее квадратичное удаление частиц от источника за время диффузии, равное отношению второго 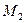и нулевого 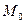моментов.

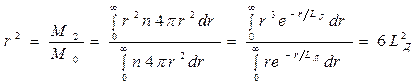(24)

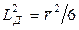
Итак, длина диффузии с точностью до постоянного сомножителя характеризует среднее квадратичное удаление частиц от места их образования.

Уравнение диффузии часто удовлетворительно описывает распределение тепловых нейтронов. Другие задачи переноса — замедление нейтронов, перенос 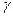- квантов — не могут быть достаточно строго описаны уравнением диффузии, в частности, потому, что в процессе замедления нейтронов и переноса 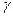- квантов происходит изменение их энергии и в связи с этим изменение сечений взаимодействия.

Однако на достаточно большом расстоянии от источника конкуренция комптоновского рассеяния (уменьшающего энергию 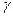-квантов) и фотоэлектрического поглощения (наиболее вероятного при малой энергии и потому вызывающего быстрое вымирание мягких 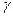-квантов) приводит к своеобразному спектральному равновесию: смягчение спектра за счет комптоновского рассеяния компенсируется более быстрым поглощением мягких квантов (следовательно, ужесточением спектра)за счет фотоэффекта. Начиная с некоторого расстояния, спектр 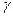- квантов, а значит, среднее сечение их взаимодействия практически становится постоянным. С увеличением расстояния уменьшается также анизотропия направления движения квантов вблизи источника вследствие их вылета по направлению радиуса-вектора и рассеяния (при больших 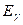), преимущественно, вперед.

Указанное выше позволяет использовать решение уравнения диффузии для приближенного описания распределения 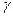- квантов на сравнительно больших расстояниях от источника.

Возрастное приближение

Возрастное приближение является удовлетворительным приближением для расчета распределения замедляющихся, в частности надтепловых, нейтронов в тяжелых (не содержащих водорода) средах. В средах с массовым числом 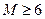средняя потеря энергии, в одном соударении, относительно невелика и процесс замедления нейтрона в первом приближении можно представить как не прерывистый, а непрерывный процесс потери энергии при его движении.

Вывод количественных соотношений теории возраста и формулировка его результатов несколько упрощаются при введении вместо энергии Е летаргии

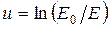
где 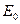— произвольное начало отсчета энергии, выбираемое обычно равно .

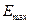Плотностью замедления 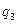называется число нейтронов (в единице объема и времени), пересекающих при замедлении некоторое заданное (пороговое) значение энергии 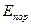или летаргии 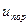. Предполагая, что поглощение нейтронов в процессе замедления отсутствует, рассмотрим в единичном объеме около точки 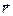баланс нейтронов, летаргия которых лежит в некотором элементарном интервале .

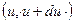Изменение плотности п таких нейтронов обусловлено при­былью нейтронов в рассматриваемый интервал летаргии за счет замедления, а также убылью 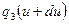из области летаргии 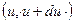вследствие дальнейшего их замедления. Другая причина изменения п — обмен нейтронами с остальной частью пространства за счет диффузии.

Разность 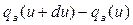, поскольку согласно условиям задачи поглощение отсутствует, должна равняться числу нейтронов 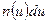с летаргией в интервале 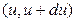, покидающих в течение 1с единичный объем около точки 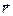вследствие диффузии, т.е. согласно рассмотренной выше при выводе уравнения диффузии величине

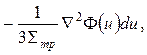
где 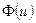— плотность потока нейтронов с летаргией, рассчитанная на единичный интервал летаргии.

Итак, соотношение баланса нейтронов имеет вид:

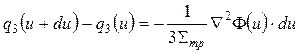
или

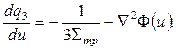
(25)

Чтобы упростить выражение (25), необходимо найти связь между переменным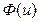и и .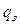

В результате одного соударения пересечь уровень летаргии могут (в предположении одинаковой потери энергии всеми нейтронами) нейтроны, летаргия которых лежит в интервале 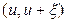. Плотность потока таких нейтронов, очевидно, равна 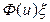, а число их соударений в единицу времени 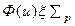. Итак,

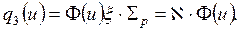(26)

Величина 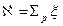, характеризующая интенсивность процессов замедления, называется замедляющей способностью.

Подстановка выражения (26) в формулу (25) приводит последнюю к виду

.

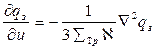Последнее уравнение можно упростить, если ввести новую переменную — фермиевский возраст нейтронов 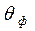— и связать ее с и уравнением

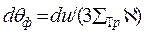. (27)

Сделав подстановку, получаем каноническую (общепринятую) (общепринятую) форму ур авнения возраста нейтронов:

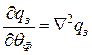. (28)

Фермиевский возраст нейтронов — величина, имеющая размерность квадрата длины. Если принять, что 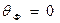для нейтронов, вылетающих из источника при начальных энергии E₀ и летаргии u_о = 0, то интегрирование уравнения (27) дает в случае монохроматического источника следующее выражение для фермиевского возраста нейтронов с летаргией и :

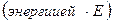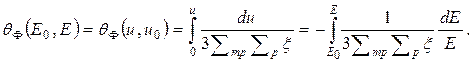(27а)

Для немонохроматических источников 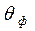получают, интегрируя 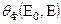по спектру источника .

Хотя возраст нейтронов — не время, но в фиксированной среде он растет с увеличением времени t₃ замедления нейтронов. Действительно, за время dt нейтрон проходит путь 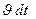, претерпевает в среднем 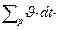соударений и, следовательно, увеличивает летаргию на величину .

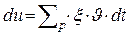Если сечения постоянны, интегрирование последнего выражения от E₀ до E с учетом того, что

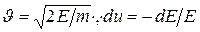
приводит к следующей формуле для времени замедления:

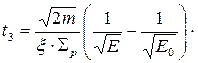(29)

В то же время интегрирование соотношения (27а) при тех же условиях постоянства сечений и индикатрис рассеяния приводит к формуле

. (28 б)

Решение уравнения возраста нейтронов (28) для точечного источника в однородной не поглощающей среде имеет вид

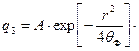(30)

Коэффициент А находится из условия нормировки.

В не поглощающей среде при стационарном источнике интеграл от плотности замедления по всему пространству (т.е. общее число нейтронов, пересекающих некоторое произвольное значение летаргии и в 1 с) равен мощности источника.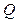

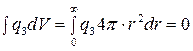
Подставив уравнение (30) в последнее соотношение и вычислив интеграл, получим:

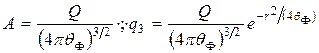(30а)

Если поглощением нейтронов в процессе замедления пренебречь нельзя, выражение (30а) умножается на вероятность 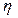избежать захвата при замедлении от 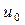до 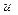. Согласно описанному выше, изменение летаргии на величину 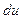, требует числа соударений 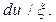Вероятность избежать захвата нейтрона при одном соударении

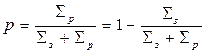
а при 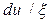соударениях по теореме умножения вероятностей .

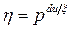Если разбить интервал замедления 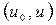на элементарные интервалы 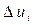, получим согласно теореме умножения вероятностей следующую вероятность избежать захвата за все время замедления:

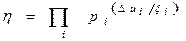
Или

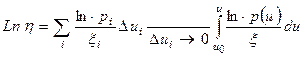(31)

Отсюда

.

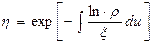При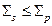

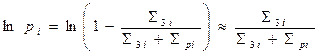
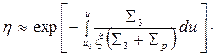(31а)

Окончательно уравнение возраста от точечного источника в поглощающей среде имеет вид

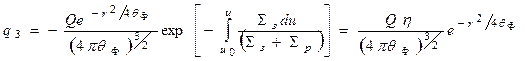.(30 б)

С учетом соотношения (26) плотность потока в единичном интервале летаргии

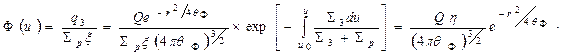(30 в)

Эти решения удовлетворительны, как указывалось, для сред с тяжелыми атомами. В средах с легкими атомами, особенно в водородсодержащей среде, распределение плотности потока замедляющихся нейтронов существенно отличается от гауссового и приближенно описывается соотношением (30) лишь на небольших расстояниях от источника точнее, при 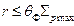, где 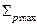— максимальное значение 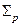на интервале 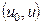. Путем использования выражения (30а) или (306) легко найти связь между 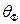и средним квадратом удаления нейтронов от источника при их замедлении. Аналогично равенству (24) и с учетом условия нормировки

,

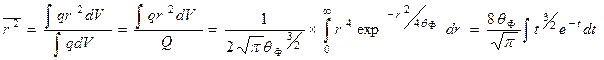где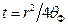

После интегрирования по частям и подстановки пределов в первом из получающихся интегралов приходим к выражению;

.

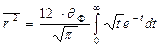Из таблиц определенных интегралов находим, что интеграл в последнем выражении равен 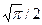, откуда

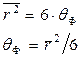(32)

Итак, возраст нейтронов с точностью до коэффициента 1/6 совпадает со средним квадратом расстояния, проходимого нейтроном при замедлении до рассматриваемой энергии.

Строго говоря, соотношения (32) справедливы лишь в средах, состоящих из тяжелых атомов. В общем случае величины 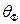и 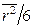не совпадают, последнюю из них называют полным возрастом или возрастом нейтронов:

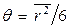(33)

Величину

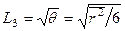(33a)

называют длиной замедления нейтронов.

В курсах нейтронной физики показано, что связаны формулой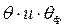

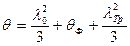(34)

где 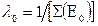— средний пробег нейтрона до первого соударения; 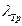— средний транспортный пробег нейтрона при конечной энергии.

Другие приближения для распределения надтепловых нейтронов

В водородсодержащих средах более удовлетворительное описание плотности замедляющихся нейтронов на больших расстояниях r от источника получается при использовании уравнения диффузии (20).

В не поглощающих средах с независящими от энергии значениями 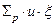можно положить по-прежнему, что коэффициент диффузии определяется выражением (15), а аналогом сечения поглощения в этом случае является сечение увода, имеющее вид,

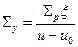(35)

если рассматривается поток нейтронов в интервале летаргии 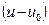. Сечение увода характеризует вероятность того, что нейтрон в результате рассеяния покинет единичный интервал летаргии и.

Очевидно, в тяжелых средах при постоянных сечениях и использовании значения 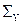в формуле (35)

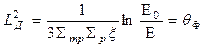
Это соотношение сохраняет силу и в случае, когда 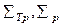и 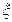зависят от энергии. Тогда решение (30) уравнения диффузии в применении к плотности замедляющихся нейтронов (в том числе надтепловых нейтронов) можно записать в виде

.

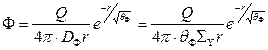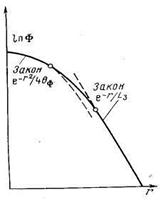
Рис. 9. Построение кривой пространственного распределения путем интерполяции («сшивания») кривых по формулам (30) и (36)

Подставляя вместо 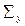его выражение из формулы (35), получаем плотность потока нейтронов с летаргией 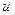, рассчитанную на единичный интервал .

.

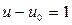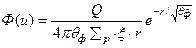В общем случае вместо 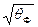используют 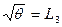Тогда

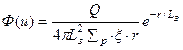(36)

Согласно эксперименту, плотность замедляющихся нейтронов при не стремится к бесконечности при 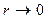, т.е. формула (36) неудовлетворительно описывает распределение замедляющихся нейтронов в окрестности источника. Однако вдали от источника 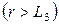в средах с высоким содержанием водорода оно оказывается близким к распределению вида (36). Поэтому часто форму распределения нейтронов в водородсодержащих средах получают путем интерполяции («сшивания») функции вида (30) при малых расстояниях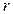и вида (36) при больших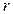(рис. 9).

Для распределения плотности надтепловых нейтронов пользуются также полуэмпирическими формулами вида

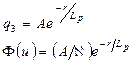, (37)

где 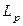- длина релаксации поля нейтронов.

Полуэмпирические формулы отражают экспериментально установленный факт экспоненциального характера распределения нейтронов во многих случаях, особенно в средах, богатых водородом. Формулы (37), (37а) называют экспоненциальным приближением. В однородной среде

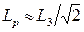(38)

Коэффициент А в непоглощающих средах легко определяется из условия нормировки

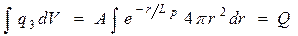
После вычисления последнего интеграла получаем:

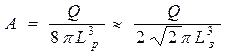. (39)

В поглощающих средах

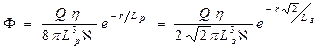(37б)

Метод групп широко используется для более точного решения задачи переноса замедления нейтронов. В этом методе рассматриваемую область изменения летаргии разбивают на ряд интервалов или энергетических групп шириной 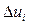Считается, что распределение нейтронов в каждой группе подчиняется диффузионному приближению.

Выведение нейтронов из каждой группы связано как с истинным поглощением, так и с процессом замедления нейтронов, поэтому вместо сечения поглощения используют сумму 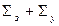Нейтроны, выбывающие из этой группы в результате замедления, играют роль источника для следующей группы. Такое последовательное изучение диффузии нейтронов в отдельных группах продолжают до достижения последней группы (обычно это группа надтепловых или тепловых нейтронов).

Приведенное выше решение уравнения (36) диффузии для процесса замедления можно рассматривать как частный случай теории групп, когда имеется всего одна группа нейтронов (одно-, групповая теория).

Пространственное распределение тепловых нейтронов вокруг точечного источника быстрых нейтронов

Распределение рассчитывается с использованием группового подхода. К группам, на которые разбивают замедляющиеся нейтроны, добавляют тепловую группу нейтронов.

Здесь ограничимся двухгрупповой теорией, когда все быстрые нейтроны рассматриваются как одна группа и плотность их за­медления до надтепловой энергии определяется, исходя из формулы (36).

Подставляя величину плотности замедления в формулу (20) вместо плотности источников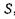, приходим к уравнению

(для всех точек, кроме ):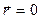

.

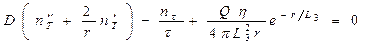Это уравнение подстановкой 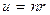, аналогичной использованному при выводе формулы (1.51), приводится к виду:

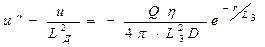(40)

Общее решение уравнения (40) без правой части имеет вид (22), причем условие обращения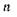в нуль при 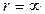требует, чтобы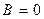

Частное решение уравнения (40) с правой частью ищем в виде

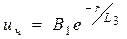
После вычисления производных 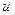подстановки их в уравнение (20) и сокращения на 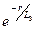приходим к соотношению:

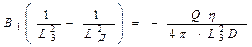
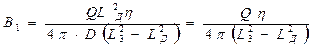(41)

Таким образом, общее решение уравнения (40) имеет вид:

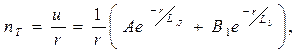
где 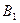определяется формулой (41).

Отсюда, используя условие нормировки и проводя необходимые преобразования, получим:

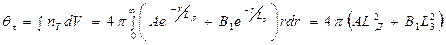
Или

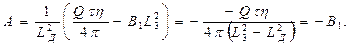
Окончательно,

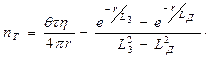(42)

Выражение (42) не теряет смысл и при 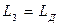,так как его раскрытие по правилу Лопиталя показывает, что

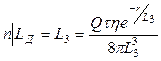, (42а)

т. е. описывается формулой типа (37а), но с заменой 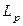на .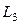

Если в уравнение диффузии (20) в качестве источника тепловых нейтронов подставить плотность замедления согласно формуле (30) или (37), то решение описывается соответственно следующими выражениями (приводим без доказательства):

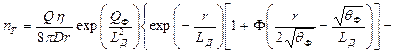(42 b)

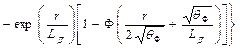
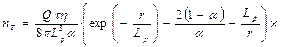
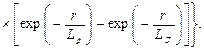(42 в)

где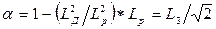

Формула (42 6), справедливая для тяжелых сред (а при малых значения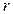и для других сред), была получена впервые Ю.П. Булашевичем. Формула (42в), предложенная С. А. Кантором, обладает преимуществами формулы (37 6) — она удовлетворительна независимо от расстояния от источника нейтронов в средах, богатых водородом.

Простота формулы (37 6) наводит на мысль попытаться использовать для описания распределения тепловых нейтронов аналогичное выражение с заменой 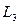на величину 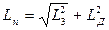равную суммарной длине миграции нейтронов в процессе замедления и диффузии, т. е. использовать соотношение

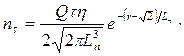(42г)

Рис.10 показывает, что это действительно возможно. При любых изменениях отношения 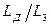различие формул (42) и (42г) до 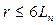не превышает 10%, что не хуже точности других формул.

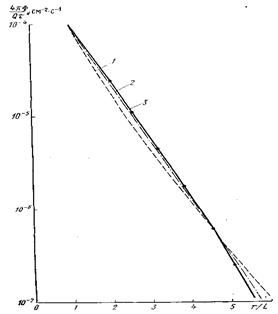
Рис. 10. Сравнение кривых пространственного распределения в различных приближениях. Формулы:

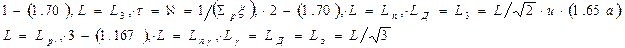
При исследовании распределения нейтронов в однородной среде от произвольно распределенных источников плотностью 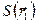вместо решения уравнений типа (20) удобнее пользоваться интегральным соотношением

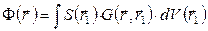, (43)

где 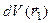— элемент объема около точки r₁;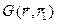- функция влияния (функция Грина) для точечного источника, представ­ляющая собой плотность нейтронов в точке 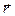создаваемая источником единичной мощности, который расположен в точке. Функция влияния — это по существу решение уравнения переноса частиц от точечного источника, находящегося в произвольной точке пространства.

Например, если рассматривается замедление нейтронов согласно уравнению возраста, то

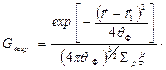(44)

Согласно уравнению диффузии

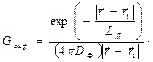(44а)

Пространственно-временное распределение нейтронов от точечного мгновенного источника

Распределение тепловых нейтронов получим, решая неста­ционарное уравнение диффузии (17б). Плотность источников

где 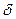— дельта-функция Дирака. Подстановка

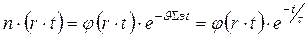
Приводит соотношение (176) к виду:

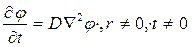
схожему с уравнениями теплопроводности и возраста. Поэтому решение получается из формулы (30а) заменой переменных 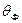на

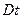
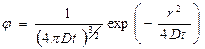
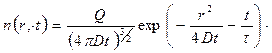(45)

Распределение тепловых нейтронов от источников быстрых нейтронов можно рассчитать с использованием интегральных соотношений типа (43), где 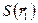заменено распределением плотности замедления 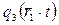от импульсного источника. Функция же влияния заменена функцией

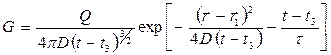(45а)

являющуюся вариантом формулы (45) для точечного источника тепловых нейтронов, включаемого в момент времени, равный времени замедления 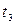Поскольку в большинстве горных пород 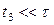, то обычно в первом приближении пренебрегают разбросом значений 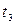и полагают

,

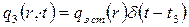где 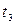— среднее время замедления, оцениваемое приближенно формулой (29), если 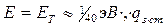, 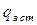— плотность замедления от стационарного источника.

При 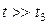можно пренебречь временем замедления t₃, т.е. считать замедление мгновенным.

Тогда

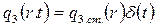
В последнем случае распределение тепловых нейтронов можно представить в виде

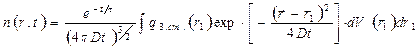(46)

Для сред с малым водородсодержанием, 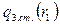описывается формулой (30). Учитывая это и вводя цилиндрическую систему координат 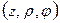, ось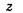, которой проходит через источник и точку наблюдения (расстояние между ними обозначим 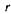), представим интеграл (46) в форме

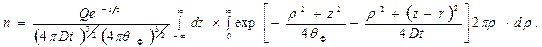
При введении обозначения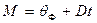

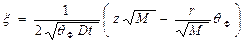
показатель экспоненты приводится к виду 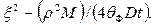После подстановки этих выражений получим:

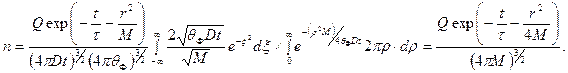(46 а)

Для сред с большим содержанием водорода в качестве 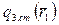можно использовать выражение (37). При этом получаются довольно сложные выражения. Их сопоставление с соотношением (46а) показало, что и в водородсодержащих средах распределение тепловых нейтронов при больших значениях t удовлетворительно описывается выражением (46а).

Согласно экспериментам и численным расчетам, при больших временах задержки влияние неоднородности, вносимой скважиной, на временное распределение нейтронов ослабевает и последнее становится подобным распределению (46а). Кроме того, при больших величинах t, как в скважине, так и в однородной среде влияние t сказывается в основном из-за множителя 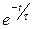, поэтому временное распределение приближенно можно описать экспоненциальной функцией

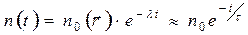
(46 6)

где 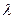— временной декремент поля затухания нейтронов.

При объединении выражений (37) и (466) пространственное временное распределение (за исключением малых значений размера зонда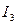и времени задержки t) описывается формулой

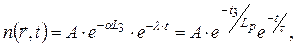(46 в)

где 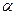— пространственный декремент затухания поля нейтронов.

Дата добавления: 2014-01-06