Физические основы

ГАММА-ГАММА-МЕТОД

При гамма-гамма-методе (ГГМ) горная порода облучается γ-квантами и регистрируется γ -излучение, достигающее детек­тора, расположенного от источника на некотором расстоянии l₃, называемом длиной зонда.

Выделяют следующие основные разновидности ГГМ: метод поглощения γ -излучения (МПГ) или метод прямого пучка, при­меняемый для изучения свойств среды, находящейся между источником и детектором, и метод рассеянного γ -излучения (МРГ), при котором среда находится вне прямой, соединяющей детектор с источником. Основной разновидностью является метод рассеянного γ - излучения. Когда говорят о ГГМ без спе­циальных оговорок, имеется в виду именно этот метод. В при­борах данного метода экран (фильтр) из тяжелого материала (железо, свинец, вольфрам и др.), установленный между источ­ником и детектором, практически полностью поглощает прямое излучение источника, и потому детектором измеряется излуче­ние, претерпевшее хотя бы одно рассеяние на атомах среды, окружающей прибор. Совокупность источника, детектора и экранов называют зондовым устройством или зондом ГГМ.

В зависимости от преобладающей энергии квантов, регист­рируемых детектором, различают плотностную (ГГМ-П) и се­лективную (ГГМ-С) модификации ГГМ. Для понимания их различия рассмотрим спектр γ -излучения вокруг источника, помещенного в горную породу.

Если бы фотоэффект не зависел от энергии, средняя энергия квантов благодаря комптоновскому рассеянию уменьшалась бы с ростом расстояния от источника. Однако интенсивное фото­электрическое поглощение мягких квантов приводит к установ­лению (начиная с некоторого расстояния) равновесного спектра, почти не изменяющегося с расстоянием. Спектр γ -излучения зависит от эффективного атомного номера Z_эф среды, а детали спектра—также от содержания отдельных элементов. Чем выше Z_эф, тем больше интенсивность фотоэффекта, шире область его преобладания и тем меньше мягких γ-квантов в спектре (рис. 1). Наличие максимумов в сечении фотоэффекта при энергии кванта, равной энергиям уровней атомов, приводит к появлению локальных минимумов в спектре, наиболее хорошо заметных в случае присутствия тяжелых элементов, напри­мер Рb. При Е_γ>1,5 —2,0 МэВ также оказывает некоторое влияние химический состав пород, обусловленное уже эффек­том образования пар.

Рис.1. Аппаратурный спектр γ-излучения в различных средах на расстояний rδ = 60 г/см² от источника ¹³⁷Cs (Е_γ = 0,66 МэВ) (по В.А.Арцыбашеву). Детектор — Nal(Th)

Рис. 2. Схемы зондов ГГМ.

1 — источник γ-излучения; 2 — детектор; 3 — свинцовый экран

Таким образом, в спектре γ-квантов можно выделить область Е_γ = 0,5—1,5 МэВ, практически нечувствительную к химиче­скому составу пород, в которой происходит почти исключи­тельно комптоновское рассеяние, а также области с Е_γ <0,1— 0,5 МэВ и Е_γ > 1,5—2,0 МэВ, где действуют и другие эффекты, зависящие от атомного номера среды.

Плотностная модификация ГГМ-П использует первую об­ласть энергий (в легких средах, характерных для разрезов нефтяных и газовых месторождений, от 0,15 до 2,0 МэВ, для более тяжелых рудных объектов область от 0,3, реже 0,6 до 1,5 МэВ). Поскольку энергия обычно применяемых источников ⁶⁰Со и ¹³⁷Cs составляет не более 1,33 МэВ, достаточно отсечь лишь область малых энергий. В боль­шинстве случаев это делают с помощью фильтров. При исследованиях в относи­тельно легких средах роль фильтра вы­полняет железный корпус зонда. Чтобы отсечь энергию на уровне Е_γ ≈0,15 МэВ, достаточно толщины корпуса, равной 3—5 мм.

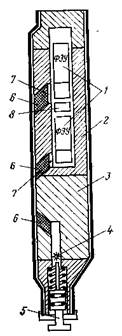
Рис. 3. Конструкция зондовой части прибора РГП-2.

1 — сцинтилляционные счетчики; 2 — экран из W; 3, 8 — экран из РЬ; 4 — источник; 5 — гидравлическое реле; 6 — коллимационные каналы; 7 — свинцово-кадмиевые экраны детекторов

При исследовании более тяжелых сред устанавливают дополнительно слои­стые экраны — снаружи из свинца, а вну­три них для поглощения характеристи­ческого рентгеновского излучения свин­ца из меди, кадмия и других более лег­ких материалов. В случае использования сцинтилляционных счетчиков отсечение мягких γ-квантов возможно и с помощью амплитудных дискриминаторов.

Селективная модификация ГГМ-С использует, наоборот, область мягкого γ -излучения. Для усиления роли фотоэффекта при этом применяют источники с энергией основных линий не более 0,4 МэВ.

Зонды ГГМ для скважин малого диаметра имеют осевую симметрию (рис. 2, а). Для скважин диаметром 59—ПО мм используют несимметричные зонды с прижимным устройством (см. рис. 2,6), позволяющие уменьшить влияние скважин. В приборах значительного диаметра, предназначенных для исследования скважин диаметром d_c > 150 мм, появляется воз­можность коллимации излучения у источника и детектора (см. рис. 2, в), что еще больше уменьшает влияние скважины и по­вышает глубинность метода.

Длину зонда ГГМ-П выбирают обычно из соотношения l_зδ =40—100 г/см², т. е. при наиболее распространенных значе­ниях δ =2,0—2,7 г/см³ l_з =15—50 см. Минимальная длина зонда ограничивается толщиной фильтра, которая для Рb дол­жна быть не менее 5—7 и 10—12 см соответственно при ис­пользовании источников ¹³⁷Cs и ⁶⁰Со. Длина зондов ГГМ-С обычно составляет 10—20 см.

Рассмотрим подробнее конструкцию зондовой части двух-зондового прижимного прибора РГП-2, используемого при исследовании плотности горных пород в нефтяных скважинах (рис. 3, а). Прибор является трехканальным и позволяет кроме кривых ГГМ-П при двух зондах длиной 17,5 и 41 см регистрировать еще диаграмму ГМ. Источник ¹³⁷Cs активностью около 100 мг-экв. Ra и два сцинтилляционных детектора раз­мещены в вольфрамовом и свинцовом экранах, имеющих кол­лимационные каналы, проходящие под углом к оси скважины от поверхности прибора (прижимаемого к стенке скважины) до источника (детектора).

Чтобы защитить обслуживающий персонал от облучения на поверхности земли и при спуске прибора в устье скважины, имеется гидравлическое реле, которое выводит источник из вольфрамового защитного экрана лишь после достижения при­бором некоторой глубины, определяемой критической величи­ной гидравлического давления промывочной жидкости. Колли­мационные окна во избежание попадания промывочной жидкости заполнены заглушками из легкого материала (поли­этилена). Между заглушками и детекторами расположены тонкие фильтры из свинца для поглощения мягкой (до 200 кэВ) компоненты γ -излучения и из Cd для поглощения характери­стического излучения Рb.

Имеются приборы с выносными прижимными зондами для уменьшения влияния скважины при значительных изменениях ее диаметра.

Зонды ГГМ-С обычно имеют цилиндрическую симметрию, коллиматоры источника и детектора выполняются в виде коль­цевых щелей, перпендикулярных к оси зонда. Применяют также зонды с коллимацией, аналогичной используемой в приборе РГП-2.

Метод поглощения γ-излучения (МПГ) заключается в про­свечивании γ -квантами среды, расположенной между источни­ком и детектором. В скважинах МПГ применяют в основ­ном для изучения плотности среды, заполняющей ствол сква­жины.

Как в методе рассеянного излучения, показания МПГ при регистрации излучения с энергией выше 0,2 МэВ зависят от плотности среды. Зависимость J _γγ = f(δ) устанавливается обычно эталонированием прибора в среде известной плотности.

Схема плотномера, т.е. прибора для измерения плотности жидкости в стволе скважины, работающего на поглощении γ -излучения, показана на рис. 4, а. На рис. 4,6, в представ­лены градуировочный график и пример диаграмм плотномера.

Для оценки Z_эф плотномер имеет два источника: мягкого излучения ¹⁰⁹Cd (Е_γ — 22 кэВ) и более жесткого ¹⁰⁷Тm. С по­мощью специальной схемы определяют интенсивность жесткого и мягкого излучений. По первому находят плотность, а по второму — Z _эф после введения поправки за плотность. Относи­тельно тяжелым элементом в среде, заполняющей скважину, является в первую очередь хлор. Поэтому такие плотномеры с двумя источниками кроме плотности среды определяют еще содержание солей хлора.

Рис. 4. Схема плотномера (а), градуировочный график (б) и диаграмма (в) плотномера (по Ю. А. Гулину, Я. Н. Басину и др.).

1 — детектор; 2 — источник; 3 — цилиндрический экран; 4 — обсадная колонна; 5 — вода; 6 — газ; 7 — насосно-компрессорная труба; J _γγв — показания ГГМ в пресной воде

Импульсный ГГМ заключается в облучении горных пород коротким импульсным потоком γ-квантов и измерении интен­сивности рассеянного излучения после импульса источника при различных временах. С увеличением времени задержки к детек­тору приходят γ -кванты, прошедшие в среде более длинный путь и в среднем проникавшие в пласт на большую глубину. Метод находится в стадии разработки.

Решение прямых задач гамма-гамма-метода

Для решения прямых задач ГГМ использовались аналити­ческие и численные методы, а также физическое моделирование. Большой объем численных расчетов методом Монте-Карло про­веден под руководством Ю. А. Гулина.

Рассмотрим два наиболее широко распространенных анали­тических метода—диффузионное приближение и приближение однократно рассеянного излучения, а затем остановимся на зависимости показаний от различных факторов, установленной по совокупности различных методов решения прямых задач.

Диффузионное приближение, как указывалось ранее, яв­ляется справедливым лишь на больших расстояниях r от источ­ника γ -квантов и границ раздела сред. На таких расстояниях можно ожидать удовлетворительного описания распределения γ-квантов диффузионным уравнением , а в однородной среде — его решением .

Имея в виду плотностную модификацию ГГМ-П и заменяя значения L_γ и τ_γ массовыми харак­теристиками, последнюю формулу представим в виде:

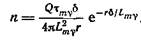(1)

Распределение γ -квантов в случае пласта, пересеченного цилиндрической скважиной радиусом R_c, характеризуется двумя уравнениями типа 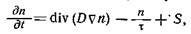записанными для пласта и скважины. В цилиндрической системе координат, ось z которой совпадает с осью скважины, а начало координат — с точечным источни­ком, эти уравнения (исключая точку р = 0, z = 0) будут иметь вид

(2)

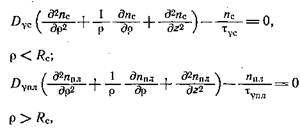
где D_γ, D_γпл — коэффициенты диффузии γ -квантов соответ­ственно в скважине и пласте; τ_γс, τ_γпл — среднее время жизни γ-квантов в тех же средах.

Граничные условия для уравнения диффузии на границе сред сводятся к требованию равенства плотностей γ-квантов и нормальных составляющих плотности их тока в бесконечно близких друг Другу точках с двух сторон границы, т. е.

(3)

Система уравнений (2) при граничных условиях (3) была решена с использованием интегрального Фурье-преобра­зования по переменной z.

Приближение однократно рассеянного излучения (лучевое приближение), использованное широко в работах А. П. Очкура и Е. М. Филиппова, оказалось полезным при качественном выяснении основных закономерностей ГГМ-П на первом этапе развития метода. При этом рассматривают лишь γ - кванты, достигающие детектора после однократного рассеяния в горной породе или скважинной среде, а вкладом многократно рассеян­ных γ -квантов пренебрегают. Такой подход удовлетворителен для небольших расстояний [до (15—20)/δ см при начальной, энергии E_γo = O,6—1,5 МэВ] от источника, где не менее 60—80 % излучения, достигшего детектора, действительно составляют γ -кванты, испытавшие лишь однократное рассеяние. Но уже на расстоянии 50/δ см эта величина составляет 20 %.

Число γ-квантов рассеявшихся в первый раз в некотором элементарном объеме dV и затем достигших точки М без дополнительного поглощения, представляет собой произведение мощности источника Q и двух вероятностей: вероятности Р₁ попадания первичного γ -кванта в объем dV, не претерпев ни одного акта рассеяния, и рассеяться в нем, и вероятности Р₂ достижения после этого единичной площадки около точки М без дополнительного рассеяния.

Плотность потока первичных γ - квантов в объеме dV опре­деляется формулой , а вероятность комптоновского рас­сеяния в этом объеме при единичном потоке равна μ _KdV. Отсюда

где μ₀ — линейный коэффициент ослабления первичного γ -излучения; r — расстояние от источника до объема dV.

Если бы рассеяние γ -кванта во все направления было равно­вероятно, вероятность Р₂ выражалась бы формулой

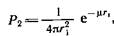
где μ — коэффициент линейного ослабления для рассеянного γ - излучения, зависящий от угла рассеяния θ; r₁ — расстояние от объема dV до точки М.

Реальное рассеяние γ - кванта не является изотропным, по­этому в последнем выражении сомножитель 1/4π следует заме­нить на коэффициент, равный вероятности рассеяния на единичный телесный угол в направлении 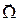. Величина дается формулой Клейна-Нишины-Тамма.

Окончательно поток излучения в точке М, обязанный рас­сеянию в объеме dV, имеет вид

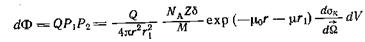(4)

поскольку μ_к/ μ_кe равно числу электронов в 1 см³, N_e = N_AZδ/M. Чтобы вычислить полную интенсивность однократно рассеянного излучения от всего пространства, введем цилиндрическую си­стему координат, начало которой совпадает с источником, а ось z — с линией, проходящей через источник и детектор. Учитывая цилиндрическую симметрию задачи, элементарные объемы dV удобно брать в виде колец радиусом ρ и сечением dρ dz. Тогда, а интеграл по всему пространству

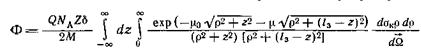(5)

где l₃ — длина зонда.

В случае пластов, пересеченных скважиной, получается сумма интегралов по отдельным однородным областям (пласт, промывочная жидкость в скважине, колонна, цемент и т. п.), а показатели экспоненты в подынтегральных выражениях заменяются на суммы и , где Δr_i и Δr_1i — части путей r и r₁, приходящиеся на отдельные области пространства.

Зависимость показаний гамма-гамма-метода от свойств пласта. Влияние скважины

Модификация ГГМ-П

Анализ формулы (1) диффузионного приближения вы­являет следующие закономерности распределения γ – квантов в однородной среде, подтверждаемые и методом Монте-Карло (рис. 5, 6). При малых значениях l_Зδ, когда значение экспо­ненциального сомножителя мало отличается от единицы, зави­симость плотности γ – квантов от плотности δ среды (в общем случае от L_γ) при l₃ = const — прямая: чем больше δ, тем выше Ф и показания ГГМ. При больших величинах l_Зδ пере­силивает экспоненциальный сомножитель: чем выше δ (меньше L_γ), тем ниже при l₃ = const показания метода. В лучевом приближении получается тот же результат.

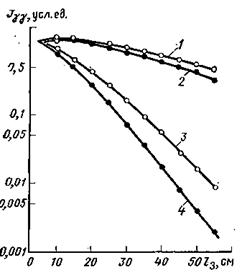
Рис. 5. Зависимость показаний _t ГГМ-П в однородной среде от длины l₃ зонда.

Расчет методом Монте-Карло (по Ю. А. Гулину и др.); среда: 1, 2 —вода, 3, 4 — пес­чаник δ=2,65 г/см³; источники: 1,3 — ⁶⁰Со (E_γо =1,25МэВ); 2, 4 — ¹³⁷Cs (E_γо = О,66 МэВ)

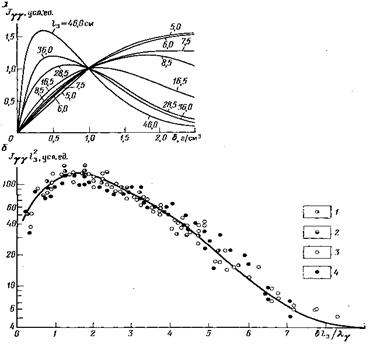
Рис. 6. Зависимость показаний ГГМ-П в однородной среде от плотности δ пород (а) и от параметра δ l₃ / λγ (б) (по К. Умиастовскому).

Источники: 1 — ²⁰³Hg, 2 — ⁷⁵Se, 3 — ¹³⁷Cs, 4 — ⁶⁰Со, λγ— длина свободного пробега γ-кванта

Зависимость показаний ГГМ от плотности среды в широком диапазоне изменений δ (при l₃ = const) не является монотонной (см. рис. 6, а). Положение максимума зависит от длины зонда и начальной энергии источника. С ростом длины зонда макси­мум сдвигается в область меньших значений δ. Положение максимума легко определить, приравняв к нулю производную от выражения (1) по δ.

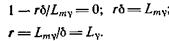(6)

Согласно рис.6 для источников ⁶⁰Со (E_γ0=1,25 МэВ) и ¹³⁷Cs (E_γ0 = 0,66 МэВ) величина L_mγ, совпадающая с инвер­сионным значением rδ, соответственно равна примерно 15 и 12 г/см². Отсюда инверсия зависимости происходит для ⁶⁰Со при δ = 1 г/см³, /₃ = 15 см, а для ¹³⁷Cs при δ = 0,5 г/см³ /₃ = = 30 см. Реально область инверсии может отличаться от указанных величин из-за неточности диффузионного приближения, влияния скважины и особенностей прибора.

Градуировочные кривые получаются более универсальными при использовании обобщенных параметров, например пара­метра μ_m l_Зδ = μl_З или параметра l_Зδ. Чтобы получить единую кривую для различных источников, некоторые авторы исполь­зуют параметр δ l_З/K(E₀)λ(E₀), где λ (Е₀) —длина свободного пробега первичного излучения, К(Е₀) —коэффициент, различ­ный для источников с разной первичной энергией квантов. За счет выбора значений К для источников ¹³⁷Cs, ²⁰³Hg, ⁷⁵Se и ⁶⁰Со построена единая кривая Ф l ²_з= f (δ l_З/K₀λ), приведенная на рис. 6, б.

Практически используют либо левую часть восходящей ветви при δ l_З <<L_mγ, либо правую ветвь при δ l_З <<L_mγ. При исследованиях скважин используют правую ветвь (l ₃ > 25— 30 см). С ростом длины зонда скорость счета экспоненциально падает (примерно в е раз на каждые 4—6 см), а чувствитель­ность ГГМ-П к плотности пород растет.

Хорошая дифференциация интенсивности γ -излучения при расположении прибора на стенке скважины большого диаметра имеет место лишь для γ -квантов, приходящих со стороны стенки скважины. Поэтому необходимо экранирование детектора со стороны скважины. Как показали расчеты методом Монте-Карло (Ю.А.Гулин и др.), угол коллимации в горизонтальной про­екции должен составлять 30—90°.

Увеличение плотности промывочной жидкости (глинистого раствора) δ _Р приводит к уменьшению показаний ГГК-П. Влия­ние изменения 6_Р на 0,2 г/см³ в скважине радиусом 10 см при­мерно такое же, как влияние изменения плотности пород на 0,35 г/см³.

Увеличение диаметра скважины обычно уменьшает среднюю плотность среды в зоне исследования и приводит (для прибо­ров без коллимации и с большими зондами) к росту показаний и уменьшению чувствительности метода к плотности пород.

Зависимость показаний приборов диффузного типа (без кол­лимации) от диаметра пустых скважин при малых зондах немонотонна. В случае малого диаметра показания, как и при больших зондах, повышаются с ростом диаметра, но затем, достигнув максимума, начинают уменьшаться.

Сильное влияние на данные ГГМ оказывает наличие про­межуточного слоя (воздух, промывочная жидкость, глинистая корка) между прижимным прибором и горной породой.

Увеличение толщины промежуточного слоя, имеющего обычно мень­шую плотность, чем порода, снижает среднюю плотность среды в зоне исследования и действует так же, как и уменьшение плотности горных пород или увеличение диаметра скважины: на доинверсионных зондах снижает показания, а на заинверсионных увеличивает. Предложен способ уменьшения влияния промежуточного слоя путем использования двойного инверсионного зонда. Он заключается в регистрации суммы показаний при двух размерах зонда — до- и послеинверсионного. Способ осуществляется двумя детекторами и одним источником или, наоборот, одним детектором и двумя источниками, расположен­ными на различном расстоянии от детектора.

В нефтяных и газовых скважинах используют в основном зонды с двумя детекторами и регистрируют раздельно их пока­зания, а влияние промежуточной зоны учитывают, совместно решая уравнения связи показаний этих зондов с плотностью среды и толщиной промежуточного слоя.

Область применения гамма-гамма-метода.

Модификация ГГМ-П применяется в основном для ре­шения следующих задач:

1) выделения в разрезе скважин горных пород с различной плотностью, определения типа пород (часто в комплексе с дру­гими методами);

2) выделения и количественного определения содержания полезных ископаемых, плотность которых отличается от плот­ности вмещающих пород;

3) определения коэффициента пористости коллекторов нефти и газа;

4) изучения технического состояния скважин.

Дата добавления: 2014-01-06