
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Чистое вращение
|
|
|
|
|   
|
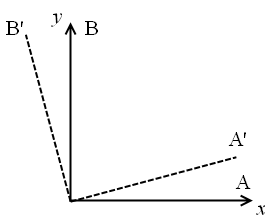
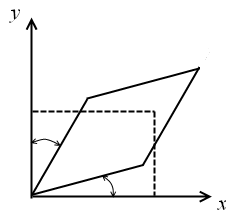
| Чистое вращение | Чистая угловая деформация |
Вращение ребер элементарного параллелепипеда приводит в общем случае как к угловой деформации элемента, так и к чистому вращению элемента как твердого тела.
Чистая угловая деформация отвечает ситуации, когда ребра вращаются с одинаковой угловой скоростью в противоположных направлениях.
Чистое вращение соответствует условию, когда ребра вращаются в одну сторону с одинаковой угловой скоростью (угол между ребрами не меняется).
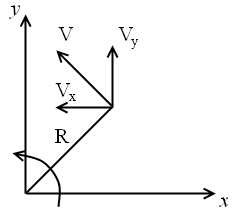
Для того чтобы получить выражения для чистого вращения напомним понятия теоретической механики. Пусть некоторое тело вращается с угловой скоростью ωz вокруг оси z.
|
Величина скорости точки тела М будет равна
 , (7.9)
, (7.9)
а ее проекции на оси x и y соответственно
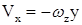 , (7.10)
, (7.10)
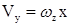 . (7.11)
. (7.11)
Определив значения  и
и 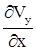 , получим
, получим
 (7.12)
(7.12)
Если аналогично рассмотрим вращение твердого тела вокруг осей x и y, то определим:
 (7.13)
(7.13)
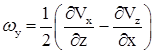 (7.14)
(7.14)
Рассмотрим, как связаны вектор угловой скорости и вектор вихря.
Выражения (7.12), (7.13), (7.14) представляют собой компоненты вектора угловой скорости. Вектор вихря определяется как векторное произведение оператора набла на вектор скорости

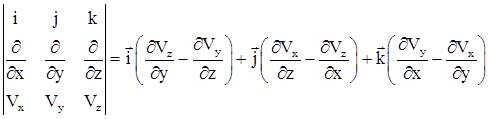 (7.15)
(7.15)
Следовательно, вектор вихря скорости жидкой частицы может быть определен вектором угловой скорости ω,
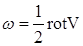 .
.
Таким образом, данная зависимость выражает связь вектора угловой скорости с вектором вихря скорости.
Физически неравенство нулю ротора скорости в какой-либо точке потока означает, что в этой точке имеет место вращение элементарного объема.
Иногда вихревое движение отождествляют с турбулентным. Это разные понятия. Вихревое движение может быть и ламинарным и турбулентным, а ламинарное и турбулентное (осредненное) движения в свою очередь могут быть как вихревыми, так и безвихревыми.
|
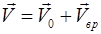 , (7.16)
, (7.16)
 - скорость поступательного движения полюса;
- скорость поступательного движения полюса;
 - скорость вращение вокруг мгновенной оси, проходящей через полюс.
- скорость вращение вокруг мгновенной оси, проходящей через полюс.

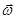 - вектор угловой скорости;
- вектор угловой скорости; 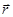 - радиус-вектор.
- радиус-вектор.
|
Скорость квазитвердотельного движения складывается из скорости поступательного и вращательного движения.
Доказательство:

|
Определим в данный момент времени поле скоростей в окрестности точки М 0 с координатами x, y, z.
Используя разложение в ряд Тейлора, можно найти значение скоростей и в точке М1(x+∆x, y+∆y, z+∆z), расположенной в окрестности точки М 0. Мы можем записать x - компоненту скорости в точке М1:
 (7.18)
(7.18)
1. Представим два последних слагаемых уравнения, состоящих из: 0,5члена+0,5члена;
2. Добавим и вычтем из этого уравнения величину
 ;
;
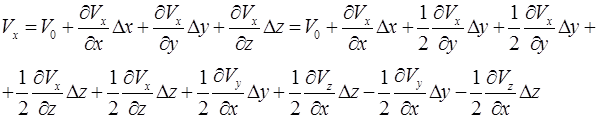 ;
;
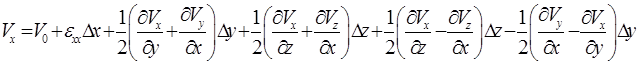 (7.19)
(7.19)
 , (7.20)
, (7.20)
 , (7.21)
, (7.21)
 . (7.22)
. (7.22)
Последние два слагаемых в полученных уравнениях представляют собой компоненты скорости, связанные с вращательным движением частицы вокруг оси. Три члена после первого в правой части уравнений представляют собой компоненты скорости деформации.
Эти три выражения можно записать в векторном виде
 , (7.23)
, (7.23)
где  - скорость поступательного движения,
- скорость поступательного движения, 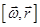 - скорость вращательного движения вокруг мгновенной оси с угловой скоростью ω,
- скорость вращательного движения вокруг мгновенной оси с угловой скоростью ω, 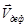 - скорость чистой деформации.
- скорость чистой деформации.
Теорема Коши-Гельмгольца:
|
Вопросы к лекции 8.
1. Из каких типов движения складывается движение жидкой частицы?
2. Какие виды деформации имеют место в случае движения жидкой частицы?
3. Приведите выражения для скорости относительной линейной деформации по различным координатам.
4. Чему равно относительное изменение удельного объема в единицу времени, выраженное через относительные линейные деформации?
5. Приведите выражения для скоростей угловой деформации?
6. Что такое чистая угловая деформация?
7. Что такое чистое угловое вращение?
8. Приведите выражения для компонент вектора угловой скорости.
9. Приведите выражения для вектора вихря скорости.
10. Как определяется вектор вихря скорости?
11. Приведите зависимость, выражающую связь вектора угловой скорости с вектором вихря скорости.
12. Приведите формулировку теоремы Шаля.
13. Приведите формулировку теоремы Коши-Гельмгольдса.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 970; Нарушение авторских прав?; Мы поможем в написании вашей работы!
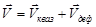 (7.17)
(7.17)